如图,已知反比例函数y= 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.
(1)试判断四边形PAOB的形状,并说明理由.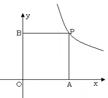
(2)连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.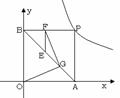
(3)若M为反比例函数y= 在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
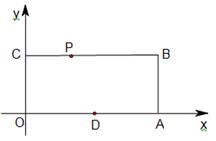
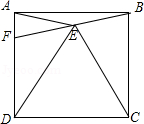
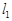 过点A(0,4),点D(4,0),直线
过点A(0,4),点D(4,0),直线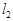 :
: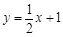 与
与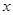 轴交于点C,两直线
轴交于点C,两直线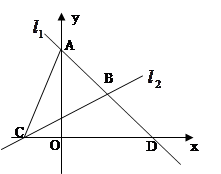
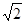 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此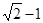 来表示
来表示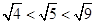 ,即
,即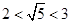 ,
,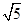 的整数部分为2,小数部分为
的整数部分为2,小数部分为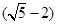 .
.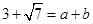 ,其中
,其中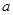 是整数,且
是整数,且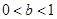 ,那么
,那么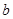 =;
=;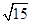 的两个整数是、,将这两个整数作为直角三角形的两条边,请你计算第三边的长度.
的两个整数是、,将这两个整数作为直角三角形的两条边,请你计算第三边的长度.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号