[湖北]2011-2012年湖北宜昌市长阳县八年级上期末复习(一)数学试卷
如果一个数的算术平方根等于它本身,那么这个数是( )
| A.0 | B.1 | C.0或1 | D.-1或0或1 |
将直角三角形的三边都扩大相同的倍数后,得到的三角形一定是( )
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.以上三种情况都有可能 |
将△ABC的三个顶点的横坐标乘以-1,纵坐标不变,则所得图形( )
| A.与原图形关于y轴对称 | B.与原图形关于x轴对称 |
| C.与原图形关于原点对称 | D.向x轴的负方向平移了一个单位 |
甲、乙两根绳共长17米,如果甲绳减去它的 ,乙绳增加1米,两根绳长相等,若设甲绳长x米,乙绳长y米,那么可列方程组 ( )
,乙绳增加1米,两根绳长相等,若设甲绳长x米,乙绳长y米,那么可列方程组 ( )
A.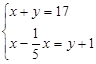 |
B.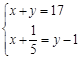 |
C.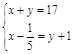 |
D. |
已知一组数据1,7,10,8,x,6,0,3,若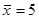 ,则x应等于 ( )
,则x应等于 ( )
| A.6 | B.5 | C.4 | D.2 |
四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠ DAB=900;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,则在下列推理不成立的是 ( )
A.①④ ⑥ ⑥ |
B.①③ ⑤ ⑤ |
C.①② ⑥ ⑥ |
D.②③ ④ ④ |
菱形的一个内角是60º,边长是5cm,则这个菱形的较短的对角线长是 ( )
A.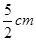 |
B.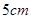 |
C.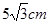 |
D.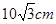 |
函数y=x图象向下平移2个单位长度后,对应函数关系式是( )
| A.y=2x | B.y=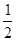 x x |
C.y="x" +2 | D.y=x-2 |
正比例函数y=(1-2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
A. <0 <0 |
B. >0 >0 |
C. < <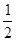 |
D.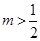 |
如图,点O是口ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于 mm.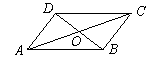
菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______.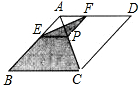
某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:
(1)这32名学生培训前考分的中位数所在的等级是 ,培训后考分的中位数所在的等级是 .
(2)这32名学生经过培训,考分等级“不合格” 的百分比由 下降到 .
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
在平面直角坐标系中(如图每格一个单位),⑴画出下列各点(-2,-1),(2,-1),(2,2),(3,2)(0,3),(-3,2),(-2,2), (-2,-1)并依次将各点连结起来(说说所连图形象什么),⑵所得图形整体向右平移2个单位,说出对应点的坐标发生了怎样的变化? 
在矩形ABCD中,EF垂直平分BD.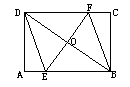
(1) 判断四边形BEDF的形状,并说明理由.
(2) 已知 BD=20,EF=15,求矩形ABCD的周长.
已知:如图,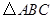 中,
中,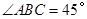 ,
, 于
于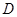 ,
, 平分
平分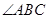 ,且
,且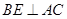 于
于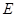 ,与
,与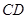 相交于点
相交于点 是
是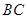 边的中点,连结
边的中点,连结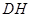 与
与 相交于点
相交于点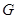 .
.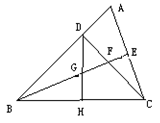
(1)求证: ;
;
(2)求证: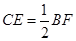 ;
;
(3) 与
与 的大小关系如何?试证明你的结论.
的大小关系如何?试证明你的结论.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.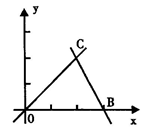
(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式.
(3)当x为何值时,直线m平分△COB的面积?
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,AF是梯 形的 高,梯形面积是49cm2,则AF= ;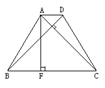
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积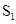 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为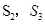 ,…,
,…,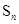 (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积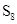 =_______。
=_______。
甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每付定价20元,乒乓球每盒定价5元。现两家商店搞促销活动。甲店:每买一付球拍赠一盒乒乓球;乙店:按定价的9折优惠。某班级需购球拍4付,乒乓球若干盒(不少于4盒)。
(1)设购买乒乓球盒数为x(盒),在甲店购买的付款数为y甲(元),在乙店购买的付款数为y乙(元),分别写出在两家商店购买的付款数与乒乓球盒数x之间的函数关系式。
(2)就乒乓球盒数讨论去哪家商店买合算?
如图,在梯形ABCD中,AB∥CD,∠BCD=90°, BD平分∠ABC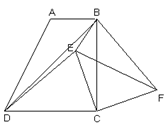
求证:(1) DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3) 在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求 的值.
的值.

 的平方根是 .
的平方根是 . ,则其边数为 ,内角和为 。
,则其边数为 ,内角和为 。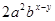 与
与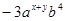 是同类项,则
是同类项,则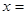 ,
, .
.

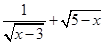 中自变量x的取值范围是_________.
中自变量x的取值范围是_________.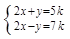 的解满足方程
的解满足方程 ,那么k的值为
,那么k的值为 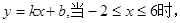 函数值的范围为
函数值的范围为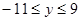 ,则此一次函数的解析式为 ;
,则此一次函数的解析式为 ;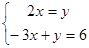 的解,点C是直线
的解,点C是直线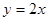 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=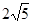
 粤公网安备 44130202000953号
粤公网安备 44130202000953号