如图,已知等边三角形 与反比例函数 的图象交于 、 两点,将 沿直线 翻折,得到 ,点 的对应点为点 ,线段 交 轴于点 ,则 的值为 .(已知

已知点,
,
,连接
,
得到矩形
,点
的边
上,将边
沿
折叠,点
的对应点为
.若点
到矩形较长两对边的距离之比为
,则点
的坐标为 .
如图,在矩形 中, , ,点 是 的中点,连接 ,将 沿直线 折叠,使点 落在点 处,则线段 的长度是

A.1B. C. D.
如图,在中,
,
,
,点
,
分别是边
,
上的动点,沿
所在的直线折叠
,使点
的对应点
始终落在边
上,若△
为直角三角形,则
的长为 .

如图,在平面直角坐标系中,坐标原点 是正方形 的一个顶点,已知点 坐标为 ,过点 , 作 轴,与边 交于点 (异于点 、 ,将四边形 沿 翻折,点 、 分别是点 、 的对应点,若点 恰好落在直线 上,则 的值等于
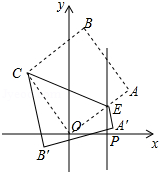
A. B. C.2D.3
如图,已知 , , ,点 为射线 上一个动点,连接 ,将 沿 折叠,点 落在点 处,过点 作 的垂线,分别交 , 于点 , .当点 为线段 的三等分点时, 的长为 .

如图,在菱形中,
,
,
为
上一动点,过
作
交
于点
,交
于点
,将
沿
折叠,使点
落在对角线
上的点
处,当△
为直角三角形时,
的长为 .

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
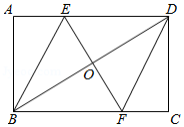
如图,四边形 是矩形, 、 分别是线段 、 上的点,点 是 与 的交点.若将 沿直线 折叠,则点 与点 重合.
(1)求证:四边形 是菱形;
(2)若 , ,求 的值.
如图,小聪用一张面积为1的正方形纸片,按如下方式操作:
①将正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,把四个等腰直角三角形扔掉;
②在余下纸片上依次重复以上操作,当完成第2019次操作时,余下纸片的面积为( )

| A. |
2 2019 |
B. |
|
C. |
|
D. |
|
对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图① ,再沿 折叠,这时发现点 恰好与点 重合(如图②
(1)根据以上操作和发现,求 的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开.求证: ;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)

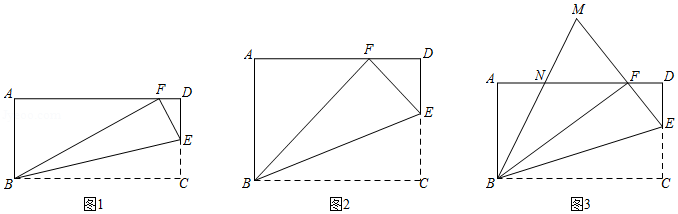
在矩形 的 边上取一点 ,将 沿 翻折,使点 恰好落在 边上点 处.
(1)如图1,若 ,求 的度数;
(2)如图2,当 ,且 时,求 的长;
(3)如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 的值.