初中数学翻折变换（折叠问题）试题

如图，将矩形 $\mathit{ABCD}$ 沿 $\mathit{AC}$ 折叠，使点 $B$ 落在点 $B\text{'}$ 处， $B\text{'}C$ 交 $\mathit{AD}$ 于点 $E$ ，若 $\angle 1=25°$ ，则 $\angle 2$ 等于 $($ 　　 $)$

A．

$25°$

B．

$30°$

C．

$50°$

D．

$60°$

实验探究：

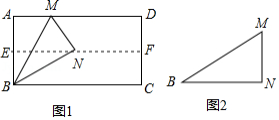
（1）如图1，对折矩形纸片 $\mathit{ABCD}$，使 $\mathit{AD}$与 $\mathit{BC}$重合，得到折痕 $\mathit{EF}$，把纸片展开；再一次折叠纸片，使点 $A$落在 $\mathit{EF}$上，并使折痕经过点 $B$，得到折痕 $\mathit{BM}$，同时得到线段 $\mathit{BN}$， $\mathit{MN}$．请你观察图1，猜想 $\angle \mathit{MBN}$的度数是多少，并证明你的结论．

（2）将图1中的三角形纸片 $\mathit{BMN}$剪下，如图2．折叠该纸片，探究 $\mathit{MN}$与 $\mathit{BM}$的数量关系．写出折叠方案，并结合方案证明你的结论．

如图，在 $△\mathit{ABC}$ 中， $\mathit{AC}＝2\sqrt{2}$ ， $\angle \mathit{ABC}＝45°$ ， $\angle \mathit{BAC}＝15°$ ，将 $△\mathit{ACB}$ 沿直线 AC翻折至 $△\mathit{ABC}$ 所在的平面内，得 $△\mathit{ACD}$ ．过点 A作 $\mathit{AE}$ ，使 $\angle \mathit{DAE}＝\angle \mathit{DAC}$ ，与 $\mathit{CD}$ 的延长线交于点 E，连接 BE，则线段 BE的长为（　　）

A．

$\sqrt{6}$

B．

3

C．

$2\sqrt{3}$

D．

4

如图，矩形纸片 $\mathit{ABCD}$ 中， $\mathit{AB}=6$ ， $\mathit{BC}=12$ ．将纸片折叠，使点 $B$ 落在边 $\mathit{AD}$ 的延长线上的点 $G$ 处，折痕为 $\mathit{EF}$ ，点 $E$ 、 $F$ 分别在边 $\mathit{AD}$ 和边 $\mathit{BC}$ 上．连接 $\mathit{BG}$ ，交 $\mathit{CD}$ 于点 $K$ ， $\mathit{FG}$ 交 $\mathit{CD}$ 于点 $H$ ．给出以下结论：

① $\mathit{EF}\perp \mathit{BG}$ ；

② $\mathit{GE}=\mathit{GF}$ ；

③ $\mathit{\Delta GDK}$ 和 $\mathit{\Delta GKH}$ 的面积相等；

④当点 $F$ 与点 $C$ 重合时， $\angle \mathit{DEF}=75°$ ，

其中正确的结论共有 $($ 　　 $)$

A．

1个

B．

2个

C．

3个

D．

4个

如图，将矩形 $\mathit{ABCD}$沿 $\mathit{GH}$对折，点 $C$落在 $Q$处，点 $D$落在 $\mathit{AB}$边上的 $E$处， $\mathit{EQ}$与 $\mathit{BC}$相交于点 $F$，若 $\mathit{AD}=8$， $\mathit{AB}=6$， $\mathit{AE}=4$，则 $\mathit{\Delta EBF}$周长的大小为　　．

如图，先有一张矩形纸片，，，点，分别在矩形的边，上，将矩形纸片沿直线折叠，使点落在矩形的边上，记为点，点落在处，连接，交于点，连接．下列结论：

①；

②四边形是菱形；

③，重合时，；

④的面积的取值范围是．

其中正确的是　　（把正确结论的序号都填上）．

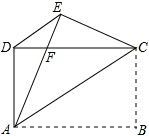
如图，矩形 ABCD中， AB＞ AD，把矩形沿对角线 AC所在直线折叠，使点 B落在点 E处， AE交 CD于点 F，连接 DE．

（1）求证：△ ADE≌△ CED；

（2）求证：△ DEF是等腰三角形．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=m$， $\mathit{BC}=n$， $m>n$，点 $P$是边 $\mathit{AB}$上一点，连接 $\mathit{CP}$，将 $\mathit{\Delta ACP}$沿 $\mathit{CP}$翻折得到 $\mathit{\Delta QCP}$．

（1）若 $m=4$， $n=3$，且 $\mathit{PQ}\perp \mathit{AB}$，求 $\mathit{BP}$的长；

（2）连接 $\mathit{BQ}$，若四边形 $\mathit{BCPQ}$是平行四边形，求 $m$与 $n$之间的关系式．

如图，在 $\text{Rt}\Delta \text{ABC}$中，点 $E$在 $\mathit{AB}$上，把这个直角三角形沿 $\mathit{CE}$折叠后，使点 $B$恰好落到斜边 $\mathit{AC}$的中点 $O$处，若 $\mathit{BC}=3$，则折痕 $\mathit{CE}$的长为 $($　　 $)$

A． $\sqrt{3}$B． $2\sqrt{3}$C． $3\sqrt{3}$D．6

如图，△ ABC中， AC＝ BC＝3， AB＝2，将它沿 AB翻折得到△ ABD，点 P、 E、 F分别为线段 AB、 AD、 DB上的动点，则 PE+ PF的最小值是（　　）

A．

$\frac{\sqrt{10}}{3}$

B．

$\frac{2\sqrt{2}}{3}$

C．

$\frac{4\sqrt{2}}{3}$

D．

$\frac{8\sqrt{10}}{3}$

如图，在边长为3的菱形 ABCD中，∠ A＝60°， M是 AD边上的一点，且 AM＝ $\frac{1}{3}$ AD， N是 AB边上的一动点，将△ AMN沿 MN所在直线翻折得到△ A′ MN，连接 A′ C．则 A′ C长度的最小值是 　　．

如图， $▱\mathit{ABCD}$中， $\mathit{AB}=2$， $\mathit{AD}=1$， $\angle \mathit{ADC}=60°$，将 $▱\mathit{ABCD}$沿过点 $A$的直线 $l$折叠，使点 $D$落到 $\mathit{AB}$边上的点 $D\text{'}$处，折痕交 $\mathit{CD}$边于点 $E$．

（1）求证：四边形 $\mathit{BCED}\text{'}$是菱形；

（2）若点 $P$是直线 $l$上的一个动点，请计算 $\mathit{PD}\text{'}+\mathit{PB}$的最小值．

如图，矩形 ABCD与菱形 EFGH的对角线均交于点 O，且 EG∥ BC，将矩形折叠，使点 C与点 O重合，折痕 MN过点 G．若 AB＝ $\sqrt{6}$ ， EF＝2，∠ H＝120°，则 DN的长为（　　）

A．

$\sqrt{6}$ - $\sqrt{3}$

B．

$\frac{\sqrt{6}+\sqrt{3}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

2 $\sqrt{3}-\sqrt{6}$

如图，矩形 $\mathit{ABCD}$ 中， $\mathit{AC}$ 与 $\mathit{BD}$ 相交于点 $E$ ， $\mathit{AD}:\mathit{AB}=\sqrt{3}:1$ ，将 $\mathit{\Delta ABD}$ 沿 $\mathit{BD}$ 折叠，点 $A$ 的对应点为 $F$ ，连接 $\mathit{AF}$ 交 $\mathit{BC}$ 于点 $G$ ，且 $\mathit{BG}=2$ ，在 $\mathit{AD}$ 边上有一点 $H$ ，使得 $\mathit{BH}+\mathit{EH}$ 的值最小，此时 $\frac{\mathit{BH}}{\mathit{CF}}=($ 　　 $)$

A．

$\frac{\sqrt{3}}{2}$

B．

$\frac{2\sqrt{3}}{3}$

C．

$\frac{\sqrt{6}}{2}$

D．

$\frac{3}{2}$

如图，平面直角坐标系中， $A(-8,0)$ ， $B(-8,4)$ ， $C(0,4)$ ，反比例函数 $y=\frac{k}{x}$ 的图象分别与线段 $\mathit{AB}$ ， $\mathit{BC}$ 交于点 $D$ ， $E$ ，连接 $\mathit{DE}$ ．若点 $B$ 关于 $\mathit{DE}$ 的对称点恰好在 $\mathit{OA}$ 上，则 $k=($ 　　 $)$

A．

$-20$

B．

$-16$

C．

$-12$

D．

$-8$