如图,把正方形纸片 沿对边中点所在的直线对折后展开,折痕为 ,再过点 折叠纸片,使点 落在 上的点 处,折痕为 .若 的长为2,则 的长为

A.2B. C. D.1
如图,将一张矩形纸片 的边 斜着向 边对折,使点 落在 上,记为 ,折痕为 ;再将 边斜向下对折,使点 落在 边上,记为 ,折痕为 , , .则矩形纸片 的面积为 .

如图,四边形 为一个矩形纸片, , ,动点 自 点出发沿 方向运动至 点后停止, 以直线 为轴翻折,点 落在点 的位置.设 ,△ 与原纸片重叠部分的面积为 .

(1)当 为何值时,直线 过点 ?
(2)当 为何值时,直线 过 的中点 ?
(3)求出 与 的函数表达式.
实验探究:
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
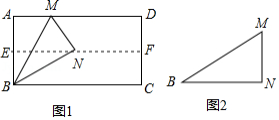
如图1,在矩形纸片 中, , ,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 、 也随之移动;
①当点 与点 重合时(如图 ,求菱形 的边长;
②若限定 、 分别在边 、 上移动,求出点 在边 上移动的最大距离.

如图,将矩形 沿 对折,点 落在 处,点 落在 边上的 处, 与 相交于点 ,若 , , ,则 周长的大小为 .

如图, 为 的 边上的中线,沿 将 折叠, 的对应点为 ,已知 , ,那么点 与 的距离为

A.3B. C. D.4
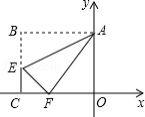
如图,在平面直角坐标系中,矩形 的边 、 分别在 轴、 轴上,点 在边 上,将该矩形沿 折叠,点 恰好落在边 上的 处.若 , ,则点 的坐标是 .
如图,点 是矩形 的边 上的点, ,将矩形沿着过点 的直线翻折后,点 、 分别落在边 下方的点 、 处,且点 、 、 在同一条直线上,折痕与边 交于点 , 与 交于点 .若 ,那么 的周长为

A. B. C. D.6
在矩形纸片 中, , , 是边 上的点,将纸片沿 折叠,使点 落在点 处,连接 ,当 为直角三角形时, 的长为 .
如图, 的面积为6, ,现将 沿 所在直线翻折,使点 落在直线 上的 处, 为直线 上的一点,则线段 的长不可能是
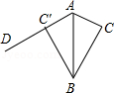
A.3B.4C.5.5D.10
如图, 是一张直角三角形纸片, ,两直角边 、 ,现将 折叠,使点 与点 重合,折痕为 ,则 .
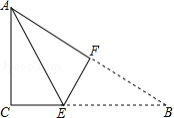
如图,把一张矩形纸片 沿 折叠后,点 落在 边上的点 处,点 落在点 处,若 ,则图中 的度数为
A. B. C. D.