如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (结果保留π).

如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°, ,则这个圆锥底面圆的半径是( )

A. B. C. D.
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则 =( )

A. B. C. D.1
如图,在扇形 AOB中∠ AOB=90°,正方形 CDEF的顶点 C是
的中点,点 D在 OB上,点 E在 OB的延长线上,当正方形 CDEF的边长为2  时,则阴影部分的面积为( )
时,则阴影部分的面积为( )

| A. |
2π﹣4 |
B. |
4π﹣8 |
C. |
2π﹣8 |
D. |
4π﹣4 |
如图, 中, 为 的中点,以 为圆心, 长为半径画一弧,交 于点 ,若 , , ,则扇形 的面积为 .

如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
(1)画出与 关于 轴对称的△ ;
(2)将 绕点 顺时针旋转 得到△ , 弧是点 所经过的路径,则旋转中心 的坐标为 ;
(3)求图中阴影部分的面积(结果保留 .

如图,在平行四边形 中, 是对角线, ,以点 为圆心,以 的长为半径作 ,交 边于点 ,交 于点 ,连接 .
(1)求证: 与 相切;
(2)若 , ,求阴影部分的面积.
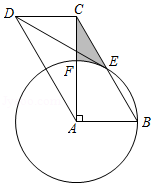
如图,点 , , 是 上的点,连接 , , ,且 ,过点 作 交 于点 ,连接 , ,已知 半径为2,则图中阴影面积为 .
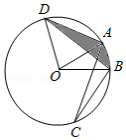
如图,在 中, , ,以点 为圆心,线段 的长为半径作 ,交 的延长线于点 ,则阴影部分的面积为 (结果保留 .

如图, 内接于 , ,点 在直径 的延长线上,且 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 ,求阴影部分的面积.

如图,在矩形 中, , , 为 上一个动点,连接 ,线段 与线段 关于 所在的直线对称,连接 ,当点 从点 运动到点 时,线段 在平面内扫过的面积为 .
