初中数学圆内接四边形的性质试题

（本题10分）如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到到B′的位置，AB′与CD交于点E.
（1）求证：△AED≌△CEB′
（2）若AB = 8，DE = 3，点P为线段AC上任意一点，PG⊥AE于G，PH⊥BC于H.求PG + PH的值.

如图，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AD＝4，AB＝5，
BC＝6，点P是AB上一个动点，当PC＋PD的和最小时，PB的长为__________．

如图，把长方形ABCD沿EF对折，若∠1=50⁰，则∠AEF的度数等于（    ）

A．25º

B．50º

C．100º

D．115º

在平行四边形ABCD中，请你添加一个条件，使它成为矩形，则你添加的条件是__________．

在平面直角坐标系中，四边形是矩形，且，在坐标轴上，满足，
．将矩形绕原点以每秒的速度逆时针旋转．设运动时间为秒，旋转过程
中矩形在第二象限内的面积为，表示与的函数关系的图象大致如右图所示，则矩形的初始位
置是（     ）

在直线l上依次摆放着七个正方形(如下图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄，则S₁＋S₂＋S₃＋S₄＝_______。

如图，在边长为1的正方形组成的网格中，的顶点均在格点上，其中点，将绕点逆时针旋转后得到．
（1）画出；
（2）在旋转过程中点所经过的路径长为          ；
（3）求在旋转过程中线段扫过的图形的面积之和．

如图，将矩形沿折叠，点恰好落在边上的点处，如果，那么值是          ．

梯形中，，，直线为梯形的对称轴，为上一点，那么的最小值         。

在△ABC中，AB=AC=5，BC=6，以AC为一边作正方形ACDE，过点D作DF⊥BC交直线BC于点F，连接AF，请你画出图形，直接写出AF的长，并画出体现解法的辅助线．

如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.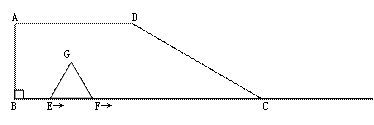

⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；
⑵若△EFG与梯形ABCD重叠部分面积是y，求
①当0＜x≤2时，y与x之间的函数关系式；
②当2＜x≤6时，y与x之间的函数关系式；
⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.

如图，P是菱形ABCD对角线BD上一点，PE⊥AB于点E，PE＝4cm，

则点P到BC的距离是_____cm.

菱形的两条对角线的长分别是6cm和8cm，则菱形的周长是__________cm．

下列关于矩形的说法，正确的是（   ）．

A．对角线相等的四边形是矩形	B．对角线互相平分的四边形是矩形
C．矩形的对角线互相垂直且平分	D．矩形的对角线相等且互相平分

一个多边形的内角和是外角和的2倍，则这个多边形的边数为(    )

A．4

B．5

C．6

D．7