2011年初中毕业升学考试(四川绵阳卷)数学
在四边形ABCD中,对角线AC、BD相交于点 O,设锐角∠DOC=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
O,设锐角∠DOC=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD是矩形时,如图1,请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(2)当四边形ABCD是平行四边形时,如图2,已知AC=BD,请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(3)当四边形ABCD是等腰梯形时,如图3,AD∥BC,此时(1)AC′与BD′的数量关系是否成立?∠AMB与α的大小关系是否成立?不必证明,直接写出结论.
如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE岁点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式; (3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形P
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形P FGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GP和正方形QCDE的边EQ落在同一条直线上.
FGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GP和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.
下面调查中,适合采用全面调查的事件是( )
| A.对全国中学生心理健康现状的调查 | B.对我市食品合格情况的调查 |
| C.对桂林电视台《桂林板路》收视率的调查 | D.对你所在的班级同学的身高情况的调查 |
在平面直角坐标系中,将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°,所得抛物线的解析式是( )
| A.y=﹣(x+1)2+2 | B.y=﹣(x﹣1)2+4 |
| C.y=﹣(x﹣1)2+2 | D.y=﹣(x+1)2+4 |
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
A. |
B. |
C. |
D. |
我市在临桂新区正在建设的广西桂林图书馆、桂林博物馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 平方米.
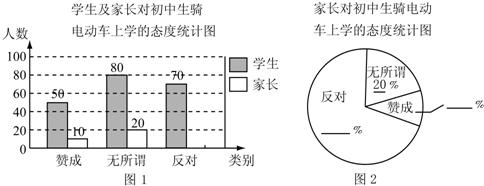
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数为 100 ;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是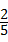 .
.
某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.
(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人?
下列运算正确的是( ).
| A.a + a2 = a3 | B.2a + 3b =" 5ab" | C.(a3)2 = a9 | D.a3÷a2 = a |
抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是( ).
| A.出现的点数是7 | B.出现的点数不会是0 |
| C.出现的点数是2 | D.出现的点数为奇数 |
将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为( ).
| A.75° | B.95° | C.105° | D.120° |

王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ).
| A.0根 | B.1根 | C.2根 | D.3根 |
下列关于矩形的说法,正确的是( ).
| A.对角线相等的四边形是矩形 | B.对角线互相平分的四边形是矩形 |
| C.矩形的对角线互相垂直且平分 | D.矩形的对角线相等且互相平分 |
灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15包.请问这次采购派男女村民各多少人?( ).
| A.男村民3人,女村民12人 | B.男村民5人,女村民10人 |
| C.男村民6人,女村民9人 | D.男村民7人,女村民8人 |
周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角a为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角b为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10 cm,则可计算出塔高约为(结果精确到0.01,参考数据: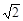 ≈1.414,
≈1.414,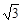 ≈1.732)( ).
≈1.732)( ).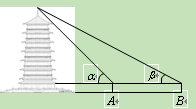
A.36.21米 B.37.71米 C.40.98米 D.42.48米
已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD = 30°,AC⊥BC,AB =" 8" cm,则△COD的面积为( ).
A. cm2 B.
cm2 B. cm2 C.
cm2 C. cm2 D.
cm2 D. cm2
cm2
若x1,x2(x1<x2)是方程(x-a)(x-b)= 1(a<b)的两个根,则实数x1,x2,a,b的大小关系为( ).
| A.x1<x2<a<b | B.x1<a<x2<b |
| C.x1<a<b<x2 | D.a<x1<b<x2 |
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-1,0),则点C的坐标为 .
鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查.
通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
(1)请你补全下面的数据统计表:
家装风格统计表
(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)
(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?
右图中曲线是反比例函数 的图象的一支.
的图象的一支.
(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)若一次函数 的图象与反比例函数的图象交于点A,与x轴交于点B,△
的图象与反比例函数的图象交于点A,与x轴交于点B,△
AOB的面积为2,求n的值.
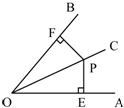
如图,在梯形ABCD中,AB∥CD,∠BAD = 90°,以AD为直径的半圆D与BC相切.
(1)求证:OB⊥OC;
(2)若AD = 12,∠BCD = 60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积.
王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
已知抛物线y = x2-2x + m-1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.



















 的值是 .
的值是 .
 ,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 
 ,
, ,
, ,…;则a2011的值为 .(用含m的代数式表示)
,…;则a2011的值为 .(用含m的代数式表示) .
. .
.
 有意义的自变量x的取值范围是( ).
有意义的自变量x的取值范围是( ).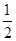
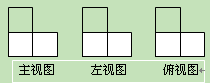
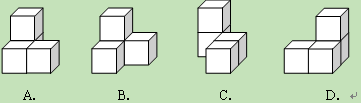



 ;
; .
. 的值;
的值; 吗?若能,求出满足条件的D点的位置;若不能,说明理由
吗?若能,求出满足条件的D点的位置;若不能,说明理由
 粤公网安备 44130202000953号
粤公网安备 44130202000953号