我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图16(1),已知格点(小正方形的顶点)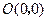 ,
,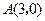 ,
,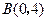 ,请你画出
,请你画出
以格点为顶点,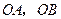 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形 ;
;
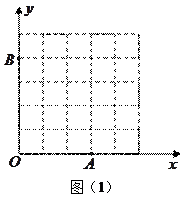 |
(3)如图16(2),将 绕顶点
绕顶点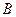 按顺时针方向旋转
按顺时针方向旋转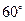 ,得到
,得到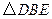 ,连结
,连结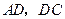 ,
,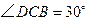 .求证:
.求证: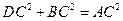 ,即四边形
,即四边形 是勾股四边形
是勾股四边形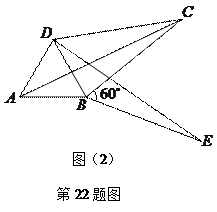
如图所示,某校在一块长40m,宽24m的土地上修一个矩形游泳池,并在四边各筑一条宽度相等的路,若游泳池的面积为720 m2,求小路的宽. 
在一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同,求这块台布的长和宽?
如图,四边形ABCD是长方形.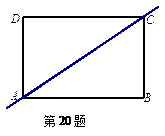
(1)作△ABC关于直线AC对称的图形;
(2)试判断(1)中所作的图形与△ACD重叠部分的三角形形状,并说明理由.
如图,AB∥CD
(1)用直尺和圆规作 的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF。要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)
(12分)
已知在菱形ABCD中,E是BC的中点,且∠FAE=∠BAE.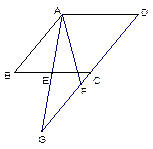
(1) 如图,当点F在边DC的延长线上时,求证:AF=BC-CF;
(2)  当点F与点C重合时,求∠B的度数,并说明理由;
当点F与点C重合时,求∠B的度数,并说明理由;
(3) 当点F在边DC上时,(1)中求证的结论还成立吗?若不成立,
请直接写出成立的结论;
(4)当∠B=90°时,请确定点F的位置
如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G。

(1)求证:△ABE≌△CBF;
(2)若∠ABE=50º,求∠EGC的大小
如图①,四边形ABCD是正方形,G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
⑴求证:DE-BF=EF.
⑵当点G为BC边中点时,试探究线段EF与GF之间的数量关系,并说明理由.
⑶若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系,并说明理由.
如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
⑴请判断四边形EFGH的形状?并说明为什么.
⑵若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
如图2,梯形ABCD中,AB∥CD,且AB=2CD,E、F分别是AB、BC的中点,EF与BD相交于点M。
⑴求证:△EDM∽△FBM
⑵若DB=9,求BM的长
本题10分)
(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。
(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
如图9,边长为5的正方形 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)( )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
的坐标;若不存在,说明理由.