初中数学圆内接四边形的性质解答题

永川区某中学为了营造良好的文化氛围，学校决定在学校的一段文化墙上制作一幅永久性的标语，为此，在文化墙上特别做了一个长1640cm的长方形横标框，铺红色衬底．为了使制作时方便、制作出来的标语美观，对有关数据作了如下规定：边空:字宽:字距=6:9:2，如图所示．

根据这个规定，若这幅标语名称的字数为14，则边空、字宽、字距各是多少?

）已知，如图，现有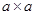、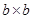的正方形纸片和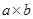的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．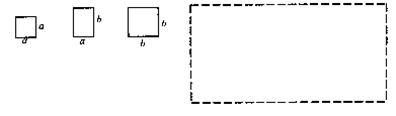

现要建造一段水坝，它的横截面是梯形ABCD，其上底CD＝4米，斜坡BC的坡度，，坝高DE＝6米.

(1)求截面梯形的面积；
(2)若该水坝的长为1000米，工程由甲、乙两个工程队同时合作完成，原计划需要25天，但在开工时，甲工程队增加了机器，工作效率提高60%，结果工程提前了5天完成，问这两个工程队原计划每天各完成多少土方？(坝的土方＝坝的横截面的面积×坝的长度)

如图17，在面积为4的平行四边形ABCD中，作一个面积为1的△ABP，使点P在平行四边形ABCD的边上（用直尺、圆规作图，保留作图痕迹，不要求写作法、证明），并写出满足条件的点P共有几个

如图，在梯形ABCD中，AD∥BC，∠B=∠ACD.

（1）证明：△ABC∽△DCA；
（2）若AC=6，BC=9，求AD长.

如图，矩形的对角线和相交于点，,试判断四边形的形状，并说明理由．

已知菱形的对角线和相交于点，，，

（1）菱形的对角线和具有怎样的位置关系？
（2）若沿两条对角线把菱形剪开，分成四个三角形，利用这四个三角形可拼成一个可以证明勾股定理的图形．请你画出示意图，并证明勾股定理．
（3）若，，求
①菱形的边长和菱形的面积．（直接写出结论）
②求菱形的高．（直接写出结论）

如图，在梯形ABCD中，AD∥BC，AB="DC" ，过点D作DE∥AB 交BC于点E．

(1) 请你判断四边形ABED的形状，并说明理由；
(2) 当△DEC为等边三角形时，
① 求∠B的度数；
② 若AD=4，DC=3，求等腰梯形ABCD的周长.

如图，在□ABCD中，AEBC，E是垂足,如果∠B＝50°，那么∠D、
∠C、∠1与∠2分别等于多少度?

如图，平面直角坐标系中，矩形的顶点在原点，点在轴的正半轴上，点在轴的正半轴上．已知，，是的中点，是的中点．

（1）分别写出点、点的坐标；
（2）过点作交轴于点，求点的坐标；
（3）在线段上是否存在点，使得以点、、为顶点的三角形是等腰三角形，若存在，求出点的坐标；若不存在，请说明理由．

如图，已知，，试说明：∥．

如图，DB∥AC，且DB=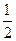AC，E是AC的中点，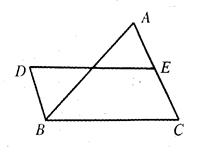

(1)求证：BC=DE；
(2)连结AD、BE，若要使四边形DBEA是矩形，则给△ABC添加一个什么条件，为什么?
(3)在（2）的条件下，若要使四边形DBEA是正方形，则∠C="        " 0

如图，在平行四边形ABCD中，∠ABC、∠BCD的平分线相交于点O，BO延长线交CD延长线于点E，

求证：OB=OE

如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，
操作示例：
我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置，构成新的图形（如图2）．
思考发现：
判断图2中四边形ABEF的形状：         ；四边形ABEF的面积是          。（用含字母的代数式表示）
实践探究：
类比图2的剪拼方法，请你就图3（已知：AB∥DC）画出剪拼成一个平行四边形的示意图．

联想拓展：
小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．
如图4，在梯形ABCD中，AD∥BC，E是CD的中点， EF⊥AB于点F，AB=5，EF=4，求梯形ABCD的面积。

如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．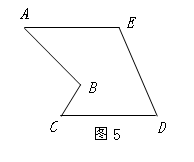

如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．

（1）设AE=x时，△EGF面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；
（2）P是MG的中点，请直接写出点P运动路线的长．