安徽省庆市江津区初二上学期期末考试七校联考数学卷
下列各组图形中,是全等形的是 ( )
| A.两个含60°角的直角三角形 | B.腰对应相等的两个等腰直角三角形 |
| C.边长为3和4的两个等腰三角形 | D.一个钝角相等的两个等腰三角形 |
等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为
| A.20° | B.70° | C.20°或70° | D.40°或140° |
如图,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是 ( )
| A.带③去 | B.带②去 | C.带①去 | D.带①和②去 |
如图,∠E=∠F=90°,∠B=∠C,AE=AF,则下列结论:①∠1=∠2;②BE=CF; ③CD=DN;④△ACN≌△ABM,其中正确的有 ( )
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于 
| A.1cm | B.2cm | C.3cm | D.4cm |
如图,线段AB的垂直平分线与BC的垂直平分线的交点P恰好在AC上,且AC=10cm,则B点到P点的距离为

如图,O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=10㎝,则△ODE的周长等于

如图,等边△ABC中,点D、E分别是边AB、AC的中点,CD、BE交于点O,则∠BOC的度数是__________

计算(每题3分,共12分):
(1)  -
- (2)
(2)  -(
-( +
+ )
)
(3) - +
+ +
+ (4) |
(4) | -
- |+|
|+| -1|-|
-1|-| -3|
-3|
利用平方根或立方根求下列x的值(每题4分,共8分):
(1) 49x2=(-4)2 (2) (x+3)3 + 53 = 0
(5分)
如图,在平面直角坐标系 中,A(1,2),B(3,1),C(-2,-1).
中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出 关于
关于 轴的对称图形
轴的对称图形 .
.
(2)写出点 的坐标(直接写答案).
的坐标(直接写答案).
A1 ______________
B1 ______________
C1 ______________
(7分)
近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P,张、李两村座落在两相交公路内(如图所示)。医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P点的位置(不写作法,保留作图痕迹)
(本题8分)
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD
求证:BE⊥AC
(10分)如图:已知在 中,
中, ,
, 为
为 边的中点,
边的中点,
过点 作
作 ,垂足分别为
,垂足分别为 .
.
(1)求证:DE=DF;
(2)若 ,BE=1,求
,BE=1,求 的周长.
的周长.
(10分)
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
(1)求证:△BCE≌△ACD;
(2)求证:FH‖BD.
如图,在等腰梯形ABCD中,AB∥CD,DC =" 3" cm,∠A=60°,BD平分∠ABC,则这个梯形的周长是…( )
| A.21 cm | B.18 cm | C.15 cm | D.12 cm |
如图,已知 ,求作一点
,求作一点 ,使
,使 到
到 的两边的距离相等,且
的两边的距离相等,且 .下列确定
.下列确定 点的方法正确的是( )
点的方法正确的是( )
 、
、 为
为 、
、 两角平分线的交点;
两角平分线的交点; 、
、 为
为 的角平分线与
的角平分线与 的垂直平分线的交点;
的垂直平分线的交点; 、
、 为
为 、
、 两边上的高的交点;
两边上的高的交点;  、
、 为
为 、
、 两边的垂直平分线的交点;
两边的垂直平分线的交点;
已知:如图,点 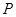 是正方形
是正方形 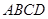 的对角线
的对角线 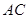 上的一个动点(
上的一个动点( 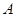 、
、 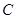 除外),作
除外),作 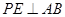 于点
于点 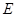 ,作
,作 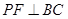 于点
于点 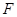 ,设正方形
,设正方形 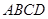 的边长为
的边长为 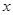 ,矩形
,矩形 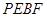 的周长为
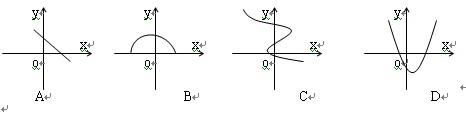
的周长为 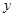 ,在下列图象中,大致表示
,在下列图象中,大致表示 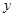 与
与 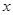 之间的函数关系的是( )
之间的函数关系的是( )

如图,过边长为 的等边
的等边 的边
的边 上一点
上一点 ,作
,作 于
于 ,
, 为
为 延长线上一点,当
延长线上一点,当 时,连
时,连 交
交 边于
边于 ,则
,则 的长为( )
的长为( )
 、
、
 、
、
 、
、
 、不能确定
、不能确定
将图甲中阴影部分的小长方形变换到图乙位置,
你能根据两个图形的面积关系得到的数学公式是________________

如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AC=

如图EB分别交AC、FC于M、D,AB、 FC交于N,
∠E=∠F=90°,∠B=∠C,AE=AF
给出下列结论:①∠1=∠2;②BE=CF; ③△ACN≌△ABM;④CD=DN。
其中正确的结论有 (填序号)

一次函数 分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
如图,AB∥CD
(1)用直尺和圆规作 的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF。要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.
能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.
供选择的三个条件(请从其中选择一个):
① ∠A=∠D;
② BC=EF;
③ AB=ED.
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴ ∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.本试卷锡
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.





 那么它的实际车牌号是:
那么它的实际车牌号是: 
 的算术平方根为_____________
的算术平方根为_____________
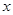 的平方根与
的平方根与 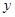 的算术平方根之积为
的算术平方根之积为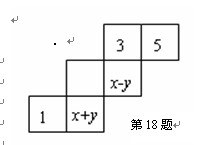
 ,
, ,
, ,
, ,
,  ,
,  中,无理数的个数是( )。
中,无理数的个数是( )。 、
、 个
个  、
、 个
个  、
、 个
个  、
、 个
个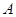 、
、
 、
、
 、
、
 、
、

 的是( )。
的是( )。  、
、
 、
、
 、
、
 、
、
 中y随
中y随 的增大而减小,则( )。
的增大而减小,则( )。 、
、
 、
、
 、
、
 、
、
 ,要说明
,要说明 ,需添加的条件不能是( )
,需添加的条件不能是( )
 、
、
 、
、
 、
、
 、
、
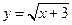 中,自变量x的取值范围是_____
中,自变量x的取值范围是_____



 关于
关于 轴对称的图形
轴对称的图形 在△
在△ 关于
关于 的坐标
的坐标 ,求代数式
,求代数式 的值
的值 ,
, 与
与 成正比,
成正比, 与
与 成正比,当
成正比,当 时,
时, ,当
,当 ,
, ,求y与x的函数解析式
,求y与x的函数解析式 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜; 粤公网安备 44130202000953号
粤公网安备 44130202000953号