某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对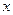 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对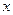 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.