广东省汕头市龙湖区初三第一学期期末数学卷
(14分)
△ABC是边长为4的等边三角形,在射线AB和BC上分别有动点P、Q,且AP=CQ,连结PQ交直线AC于点D, 作PE⊥AC,垂足为E.
作PE⊥AC,垂足为E.
(1)如图,当点P在边AB(与点A、B不重合)上,问:
①线段PD与线段DQ之间有怎样的大小关系?试证明你的结论.
②随着点P、Q的移动,线段DE的长能否确定?若能,求出DE
的长,若不能,简要说明理由;
(2)当点P在射线AB上,若设AP=x,CD=y,求:
①y与x之间的函数关系式,并写出x的取值范围;
②当x为何值时,△PCQ的面积与△ABC的面积相等.
如图,已知 ,求作一点
,求作一点 ,使
,使 到
到 的两边的距离相等,且
的两边的距离相等,且 .下列确定
.下列确定 点的方法正确的是( )
点的方法正确的是( )
 、
、 为
为 、
、 两角平分线的交点;
两角平分线的交点; 、
、 为
为 的角平分线与
的角平分线与 的垂直平分线的交点;
的垂直平分线的交点; 、
、 为
为 、
、 两边上的高的交点;
两边上的高的交点;  、
、 为
为 、
、 两边的垂直平分线的交点;
两边的垂直平分线的交点;
已知:如图,点 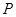 是正方形
是正方形 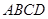 的对角线
的对角线 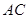 上的一个动点(
上的一个动点( 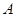 、
、 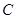 除外),作
除外),作 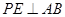 于点
于点 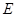 ,作
,作 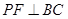 于点
于点 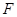 ,设正方形
,设正方形 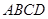 的边长为
的边长为 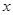 ,矩形
,矩形 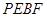 的周长为
的周长为 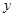 ,在下列图象中,大致表示
,在下列图象中,大致表示 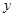 与
与 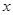 之间的函数关系的是( )
之间的函数关系的是( )

如图,过边长为 的等边
的等边 的边
的边 上一点
上一点 ,作
,作 于
于 ,
, 为
为 延长线上一点,当
延长线上一点,当 时,连
时,连 交
交 边于
边于 ,则
,则 的长为( )
的长为( )
 、
、
 、
、
 、
、
 、不能确定
、不能确定
将图甲中阴影部分的小长方形变换到图乙位置,
你能根据两个图形的面积关系得到的数学公式是________________

如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AC=

如图EB分别交AC、FC于M、D,AB、 FC交于N,
∠E=∠F=90°,∠B=∠C,AE=AF
给出下列结论:①∠1=∠2;②BE=CF; ③△ACN≌△ABM;④CD=DN。
其中正确的结论有 (填序号)

一次函数 分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个
如图,AB∥CD
(1)用直尺和圆规作 的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF。要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.
能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.
供选择的三个条件(请从其中选择一个):
① ∠A=∠D;
② BC=EF;
③ AB=ED.
平面直角坐标系内一点P(2,-3)关于原点对称点的坐标是( )
| A.(3,-2) | B.(2,3) | C.(-2,3) | D.(2,-3) |
已知⊙O1和⊙O2的半径分别为3cm和4cm,两圆的圆心距O1O2=5cm,则⊙O1和⊙O2的位置关系为( )
| A.相离 | B.外切 | C.相交 | D.内切 |
关于 的方程
的方程 的根的情况是( )
的根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 | C.没有实数根 | D.不能确定 |
如图,在⊙O中,弦AB、CD相交于点P,∠A=40°,∠APD=75°,则∠B=
A.15° B.35° C.40° D.75°
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为___________.(用含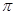 的代数式表示)
的代数式表示)
(1)探究下表中的奥秘,并完成填空:
| 一元二次方程 |
根 |
二次三项式 |
 |
 |
 |
 |
 |
 |
 |
________________ |
 |
 |
 |
 |
 |
_________________ |
 |
(2)仿照上表把二次三项式 (其中
(其中 )进行分解?
)进行分解?
在一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同,求这块台布的长和宽?
如图,已知抛物线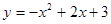 与
与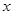 轴的两个交点为A、B,与
轴的两个交点为A、B,与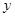 轴交于点C
轴交于点C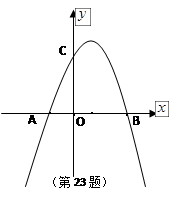
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
 ,
, ,
, ,
, ,
,  ,
,  中,无理数的个数是( )。
中,无理数的个数是( )。 、
、 个
个  、
、 个
个  、
、 个
个  、
、 个
个 、
、
 、
、
 、
、
 、
、

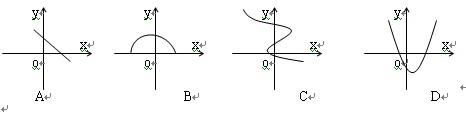
 的是( )。
的是( )。  、
、
 、
、
 、
、
 、
、
 中y随
中y随 的增大而减小,则( )。
的增大而减小,则( )。 、
、
 、
、
 、
、
 、
、
 ,要说明
,要说明 ,需添加的条件不能是( )
,需添加的条件不能是( )
 、
、
 、
、
 、
、
 、
、
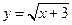 中,自变量x的取值范围是_____
中,自变量x的取值范围是_____



 关于
关于 轴对称的图形
轴对称的图形 在△
在△ 关于
关于 的坐标
的坐标 ,求代数式
,求代数式 的值
的值 ,
, 与
与 成正比,
成正比, 与
与 成正比,当
成正比,当 时,
时, ,当
,当 ,
, ,求y与x的函数解析式
,求y与x的函数解析式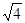 的值是( )
的值是( )
 ,则正六边形的边长为( )
,则正六边形的边长为( )




 有意义的
有意义的 的取值范围是_______
的取值范围是_______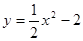 的图象上的一个点,写出一个
的图象上的一个点,写出一个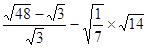
 ,其中
,其中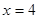
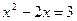


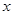 (0<
(0<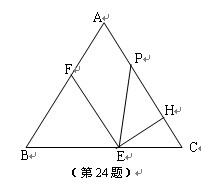
 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 粤公网安备 44130202000953号
粤公网安备 44130202000953号