初中数学圆内接四边形的性质解答题

已知如图，AD∥BC，∠1＝∠3，求证：∠B＝∠D

如图，四边形ABCD是平行四边形，EF分别是BC、AD上的点，∠1=∠2.
求证：△ABE≌△CDF.

如图，在中，点、、分别在、、上，，，且是的中点．求证：

已知：如图，点E、F分别为□ABCD 的BC、AD边上的点，且∠1=∠2.
求证：AE=FC.

如图，在菱形ABCD中，AB=2，,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为          时，四边形AMDN是矩形；
②当AM的值为          时，四边形AMDN是菱形。

如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，BD分别与AE、AF相交于G、H．

（1）在图中找出与△ABE相似的三角形，并说明理由；
（2）若AG=AH，求证：四边形ABCD是菱形．

如图，△ABC是等腰三角形，AB＝BC，点D为BC的中点．

（1）用圆规和没有刻度的直尺作图，并保留作图痕迹：
①过点B作AC的平行线BP；
②过点D作BP的垂线，分别交AC，BP，BQ于点E，F，G．
（2）在（1）所作的图中，连接BE，CF．求证：四边形BFCE是平行四边形．

如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，求电视塔的高ED。

如图，利用一面足够长的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏），设矩形ABCD的宽AD为x米，矩形的长为AB（且AB＞AD）．

（1）若所用铁栅栏的长为40米，用含x的代数式表示矩形的长AB；
（2）在（1）的条件下，若使矩形场地面积为192平方米，则AD、AB的长应分别为多少米？

如图，矩形ABCD中，点E，F分别在AB，CD边上，连接CE、AF，∠DCE=∠BAF．试判断四边形AECF的形状并加以证明．

在Rt△ABC中，∠ACB=90°，AB=4，D为AB的中点，将一直角△DEF纸片平放在△ACB所在的平面上，且使直角顶点重合于点D（C始终在△DEF内部），设纸片的两直角边分别与AC、BC相交于M、N.
当∠A=∠NDB=45°时，四边形MDNC的面积为       ；
当∠A=45°，∠NDB≠45°时，四边形MDNC的面积是否与（1）相同？说明理由；
当∠A=∠NDB=30°时，四边形MDNC的面积为       ；
当∠A=30°，∠NDB≠30°时，四边形MDNC的面积是否发生变化？若不发生变化（即与（3）相同），说明理由，若发生变化，设四边形MDNC的面积为S，BN为，求S与之间的关系.

已知：如图，在直角梯形中，，，，．
求直角梯形的面积；
点E是边上一点，过点作EF⊥DC于点F.求证．

如图,矩形ABCD的对角线相交于点O,DE∥AC,CE//BD．求证：四边形OCED是菱形．

如图1，在□ABCD中，AH⊥DC，垂足为H，AB=4，AD=7，AH=．现有两个动点E，F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E，F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，点G在射线AB上，当点E运动到点C时，E，F两点同时停止运动，设运动时间为t秒．
    
（1）试求出当点G与点B重合时t的值；
（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请求出S与t之间的函数表达式，并写出相应的自变量t的取值范围；
（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度α（0°＜α＜360°），在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′，设直线F′G′与射线DC、射线AC分别相交于M，N两点．试问：是否存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出CM的长度；若不存在，请说明理由．

如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．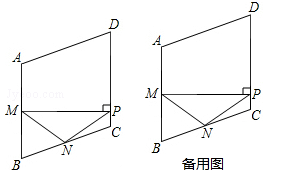

（1）若∠B=60°，这时点P与点C重合，则∠NMP=       度；
（2）求证：NM=NP；
（3）当△NPC为等腰三角形时，求∠B的度数．