如图,在矩形ABCD中,AD=8,AB=6,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时停止运动,点Q也随之停止,设点P,Q运动的时间是t秒(t>0)
(1)用含t的代数式表示线段BQ的长;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,求S与t之间的函数关系式;
(3)连接AC,当正方形PQEF与△ADC重叠部分为三角形时,直接写出t的取值范围.
四边形ABCD为菱形,点P为对角线BD上的一个动点.
(1)如图1,连接AP并延长交BC的延长线于点E,连接 PC,求证:∠AEB=∠PCD.
(2)如图1,当PA=PD且PC⊥BE时,求∠ABC的度数.
(3)连接AP并延长交射线BC于点E,连接 PC,若∠ABC=90°且△PCE是等腰三角形,求∠PEC的度数.
已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
如图,矩形ABCD,E是AB上一点,且DE=AB,过C作CF⊥DE于F.
(1)猜想:AD与CF的大小关系;
(2)请证明上面的结论.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径.
在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:四边形ABCD是平行四边形.
某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下:阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.
(1)设一块绿化区的长边为xm,写出工程总造价y与x的函数关系式(写出x的取值范围).
(2)如果小区投资46.9万元,问能否完成工程任务?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考值: )
)
如图,点E,F分别在正方形ABCD的边DA,DC延长线上,且AE﹣CF,连接BE,BF,过点E作EG∥BF,过点F作FG∥BE,EG,FG交于点G.
(1)求证:△ABE≌△CBF;
(2)求证:四边形BEGF是菱形;
(3)若AD=3AE=3,求四边形BEGF的周长.
如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
(如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.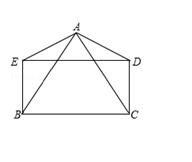
求证:四边形BCDE是矩形.
如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且DF=BE.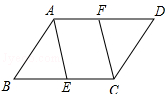
求证:AE=CF.
如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为 ,求EF的值.
,求EF的值.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.