某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下:阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.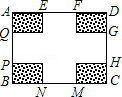
(1)设一块绿化区的长边为xm,写出工程总造价y与x的函数关系式(写出x的取值范围).
(2)如果小区投资46.9万元,问能否完成工程任务?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考值: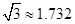 )
)
相关知识点
推荐套卷

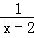 =
=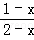 ﹣3
﹣3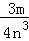 )÷(﹣
)÷(﹣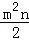 )
) .
. ﹣ab的值.
﹣ab的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号