[江苏]2005年初中毕业升学考试(江苏常州卷)数学
如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于 cm,四边形EFGH的面积等于 cm2. 
10张卡片分别写有0至9十个数字,将它们放入纸箱后,任意摸出一张,则P(摸到数字2)= ,P(摸到奇数)= .
已知抛物线 的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线 向 平移 个单位,则得到抛物线
向 平移 个单位,则得到抛物线 .
.
将100个数据分成8个组,如下表:
| 组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 频树 |
11 |
14 |
12 |
13 |
13 |
x |
12 |
10 |
则第六组的频数为
A、12 B、13 C、14 D、15
下面是一天中四个不同时刻两个建筑物的影子:
将它们按时间先后顺序进行排列,正确的是
| A.③④②① | B.②④③① | C.③④①② | D.③①②④ |
如图,已知AB∥CD,直线 分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是
分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是 
A、60° B、70° C、80° D、90°
如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于
| A.44° | B.68° | C.46° | D.22° |
如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积是 
A. |
B. |
C. |
D. |
若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,则正方体的个数至少是 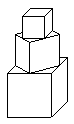
| A.2 | B.3 | C.4 | D.5 |
某水电站的蓄水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.已知某天0点到6点,进行机组试运行,试机时至少打开一个水口,且该水池的蓄水量与时间的关系如图丙所示:
给出以下3个判断:
①0点到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水不出水. 则上述判断中一定正确的是
| A.① | B.② | C.②③ | D.①②③ |
如图,已知 为等边三角形,
为等边三角形, 、
、 、
、 分别在边
分别在边 、
、 、
、 上,且
上,且 也是等边三角形.
也是等边三角形.
(1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的;
(2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.
有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上);
(1)两次测试最低分在第 次测试中;
(2)第 次测试较容易;
(3)第一次测试中,中位数在 分数段,第二次测试中,中位数在 分数段.
某中学七年级有6个班,要从中选出2个班代表学校参加某项活动,七(1)班必须参加,另外再从七(2)至七(6)班选出1个班.七(4)班有学生建议用如下的方法:从装有编号为1、2、3的三个白球 袋中摸出1个球,再从装有编号为1、2、3的三个红球
袋中摸出1个球,再从装有编号为1、2、3的三个红球 袋中摸出1个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你人为这种方法公平吗?请说明理由.
袋中摸出1个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你人为这种方法公平吗?请说明理由.
如图,在 中,
中, ,
, ,
, .
.
(1)在方格纸①中,画 ,使
,使 ∽
∽ ,且相似比为2︰1;
,且相似比为2︰1;
(2)若将(1)中 称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点
称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点 为对称中心,并且以直线
为对称中心,并且以直线 为对称轴的图案.
为对称轴的图案.
如图,有一木制圆形脸谱工艺品, 、
、 两点为脸谱的耳朵,打算在工艺品反面两耳连线中点
两点为脸谱的耳朵,打算在工艺品反面两耳连线中点 处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点
处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点 的位置(画出图形表示),并且分别说明理由.
的位置(画出图形表示),并且分别说明理由.
理由是:
七(2)班共有50名学生,老师安排每人制作一件 型或
型或 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36 ,乙种制作材料29
,乙种制作材料29 ,制作
,制作 、
、 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
| |
需甲种材料 |
需乙种材料 |
1件 型陶艺品 型陶艺品 |
0.9 |
0.3 |
1件 型陶艺品 型陶艺品 |
0.4 |
1 |
(1)设制作 型陶艺品
型陶艺品 件,求
件,求 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作 型和
型和 型陶艺品的件数.
型陶艺品的件数.
 的相反数是 ,
的相反数是 ,  ,
, .
. . (保留4个有效数字)
. (保留4个有效数字)


 ;
; 
 ;
; 
 中,点
中,点 、
、 、
、 分别在
分别在 、
、 、
、 上,
上, ,
, ,且
,且

 ,
, ,
,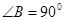 ,
, ,将它放在直角坐标系中,使斜边
,将它放在直角坐标系中,使斜边 在
在 轴上,直角顶点
轴上,直角顶点 在反比例函数
在反比例函数 的图象上,求点
的图象上,求点 的坐标.
的坐标.
 的半径为1,以
的半径为1,以 ,顶点
,顶点 的坐标为(
的坐标为( ,0),顶点
,0),顶点 在
在 轴上方,顶点
轴上方,顶点 在⊙
在⊙
 与⊙
与⊙ 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由; ,求出
,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号