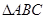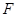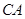如图，已知为等边三角形，、、分别在边、、上，且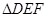也是等边三角形

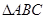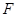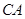如图，已知为等边三角形，、、分别在边、、上，且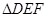也是等边三角形．
（1）除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的；
（2）你所证明相等的线段，可以通过怎样的变化相互得到？写出变化过程．

相关试题

某校为了解七年级学生的体重情况，随机抽取了七年级 $m$ 名学生进行调查，将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图．

请根据图表信息回答下列问题：

（1）填空：

① $m =$ 　　，

② $n =$ 　　，

③在扇形统计图中， $C$ 组所在扇形的圆心角的度数等于　　度；

（2）若把每组中各个体重值用这组数据的中间值代替（例如： $A$ 组数据中间值为40千克），则被调查学生的平均体重是多少千克？

（3）如果该校七年级有1000名学生，请估算七年级体重低于47.5千克的学生大约有多少人？

收藏答案/解析

如图，一艘船由 $A$ 港沿北偏东 $60 °$ 方向航行 $10 km$ 至 $B$ 港，然后再沿北偏西 $30 °$ 方向航行 $10 km$ 至 $C$ 港．

（1）求 $A$ ， $C$ 两港之间的距离（结果保留到 $0.1 km$ ，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732)$ ；

（2）确定 $C$ 港在 $A$ 港的什么方向．

收藏答案/解析

某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同，求该工厂原来平均每天生产多少台机器？

收藏答案/解析

已知直线 $y = \frac{1}{2} x + 2$ 分别交 $x$ 轴、 $y$ 轴于 $A$ 、 $B$ 两点，抛物线 $y = \frac{1}{2} x^{2} + mx - 2$ 经过点 $A$ ，和 $x$ 轴的另一个交点为 $C$ ．

（1）求抛物线的解析式；

（2）如图1，点 $D$ 是抛物线上的动点，且在第三象限，求 $ΔABD$ 面积的最大值；

（3）如图2，经过点 $M (- 4, 1)$ 的直线交抛物线于点 $P$ 、 $Q$ ，连接 $CP$ 、 $CQ$ 分别交 $y$ 轴于点 $E$ 、 $F$ ，求 $OE \cdot OF$ 的值．

备注：抛物线顶点坐标公式 $(- \frac{b}{2 a}$ ， $\frac{4 ac - b^{2}}{4 a})$

收藏答案/解析

如图，在矩形 $ABCD$ 中， $AD = 5$ ， $CD = 4$ ，点 $E$ 是 $BC$ 边上的点， $BE = 3$ ，连接 $AE$ ， $DF ⊥ AE$ 交于点 $F$ ．

（1）求证： $ΔABE ≅ ΔDFA$ ；

（2）连接 $CF$ ，求 $\sin ∠ DCF$ 的值；

（3）连接 $AC$ 交 $DF$ 于点 $G$ ，求 $\frac{AG}{GC}$ 的值．

收藏答案/解析