初中数学圆内接四边形的性质解答题

如图，在Rt△ABC中，D、F分别是AB、AC的中点，延长BC到点E，使
求证：四边形DEBF是等腰梯形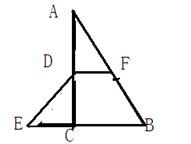

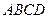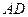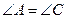如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形是平行四边形，并予以证明．（写出一种即可）关系：①∥，②，③，④．
]
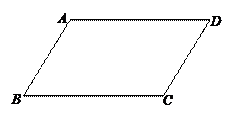
已知：在四边形中，　　　　　，　　　　　；
求证：四边形是平行四边形．

如图，ABCD的两条对角线线交于O，且。
问：⑴
⑵四边形ABCD是菱形？为什么？

如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F，且AF=BD，连接BF.
（1）求证：D是BC的中点.
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论.

(10分)如图，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC.

（1）试猜想AE与GC有怎样的位置关系，并证明你的结论；
（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图，连接AE和GC. 你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由.

如图（1），点M、N分别是正方形ABCD的边AB、AD的中点，连接CN、DM．
（1）判断CN、DM的数量关系与位置关系，并说明理由；
（2）如图（2），设CN、DM的交点为H，连接BH，求证：△BCH是等腰三角形；
（3）将△ADM沿DM翻折得到△A′DM，延长MA′交DC的延长线于点E，如图（3），求tan∠DEM．

(本题满分12分)

(本题满分8分)
已知：如图,四边形ABCD是平行四边形,△ADE和△BCF都是等边三角形.
求证:BD和EF互相平分.

如图，直角梯形ABCD中，AD∥BC，∠ABC＝90°，已知AD＝AB＝3，BC＝4，动点P从B点出发，沿线段BC向点C作匀速运动；动点Q从点D 出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．
(1) 求NC，MC的长(用t的代数式表示)；
(2) 当t为何值时，四边形PCDQ构成平行四边形？
(3) 当t为何值时,射线QN恰好将△ABC的面积平分？
并判断此时△ABC的周长是否也被射线QN平分.

如图，已知一矩形ABCD，若把△ABE沿折痕BE向上翻折，A点恰好落在DC上，设此点为F，且这时AE:ED=5:3，BE=5，这个矩形的长宽各是多少？

如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4， E为AB中点，EF∥DC交BC于点F， 求EF的长

（本大题共6分）如图，在梯形ABCD中，AD//BC，∠B＝90°，AB＝14 cm，AD＝18cm，BC＝21cm，点P从点A出发沿AD边向点D以1 cm／s的速度移动，点Q从点C出发沿CB向点B以2 cm/s的速度移动，若点P、Q分别从点A、C同时出发，设移动时间为t s，则t为何值时，梯形PQCD是等腰梯形？

(满分l0分)如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点E处，求证：EF=DF．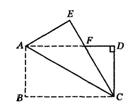

(满分l0分)如图，在△ABC中，∠ACB=90°，点E为AB中点，连结CE，过点E作ED上BC于点D，在DE的延长线上取一点F，使得AF=CE，求证：四边形ACEF是平行四边形。

(满分l2分)如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2．点O是AC的中点，过点O的直线x从与AC重合的位置开始，绕点O作逆时针旋转，交AB边于点D．过点C作CE∥AB交直线l于点E，设直线l的旋转角为a．
(1)①当a=______°时，四边形EDBC是等腰梯形，此时AD的长为_________；
②当a=______°时，四边形EDBC是直角梯形，此时AD的长为_________；
(2)当a=90°时，判断四边形EDBC是否为菱形，并说明理由。