如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图(2),设CN、DM的交点为H,连接BH,求证:△BCH是等腰三角形;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图(3),求tan∠DEM.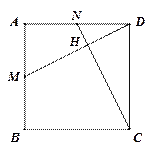


相关知识点
推荐套卷
如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图(2),设CN、DM的交点为H,连接BH,求证:△BCH是等腰三角形;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图(3),求tan∠DEM.

