初中数学圆内接四边形的性质解答题

（本题8分）
如图，在梯形ABCD中，AD∥BC，∠ABC、∠BCD的平分线正好相交于梯形的中位线EF上的点G。
试说明：△BEG是等腰三角形；（4分。）
若EF=2，求梯形的周长。（4分。）

如图，延长□ABCD的边DC到E，使CE=CD，连结AE交BC于点F。
（1）试说明：△ABF≌△ECF；（4分。）
（2）连结AC、BD相交于点O，连结OF，问OF与AB有怎样的数量关系与位置关系，说明理由。（4分。）
 

已知：如图，在□ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC

求证：BE＝DG
若∠B＝60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？说明你的理由．

如图(1)在梯形ABCD中，AD∥BC，且AD＝4cm，AB＝6cm，BC=12cm，DC＝10cm.若动点P从A点出发，以每秒4cm的速度沿线段AD、DC向C点运动；动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时，动点P、Q同时停止运动. 设点P、Q同时出发，并运动了t秒.
 
求梯形ABCD的面积.
当t为何值时，四边形PQCD成为平行四边形？
是否存在t，使得P点在线段DC上，且PQ⊥DC（如图(2)所示）？若存在，求出此时t的值，若不存在，说明理由

如图，在梯形ABCD中，AB∥DC，AD=BC，点E是CD延长线上一点，且AE∥BD．

判断四边形ABDE是怎样的四边形，说明理由
△ACE是等腰三角形吗？请说明理由

已知正方形ABCD的边长为6cm，E、F分别为BC、CD上的点，且E为BC的中点，DF：FC=1：2。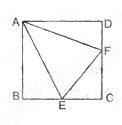

△AEF的周长
△AEF的面积
△AEF中EF边上的高。

一个工人师傅要将一个正方形（四个角都是直角，四边都相等，边长的余料，修剪成如四边形的零件. 其中，是的中点.

试用含的代数式表示的值；
连接，则△是直角三角形吗？为什么？

如图四边形ABCD中，∠B=90º，AB=4，BC=3。CD=13，AD=12，
求四边形ABCD的面积

长方形纸片EFGH可以绕着长方形纸片ABCD上的点O自由的旋转，当边EH与AB相交时，形成了∠1，∠2，求∠1+∠2的度数。（长方形的每个角都是直角且对边平行）

如图，四边形ABCD中，AD∥BC，∠ABD=30^o，
AB=AD，DC⊥BC于点C，若BD=2，求CD的长.

已知：如图，在正方形中，是上一点，延长到，使，连接并延长交于．
求证：；
将绕点顺时针旋转得到，
判断四边形是什么特殊四边形？并说明理由．

（本题9分）
如图1，在△ABC中，AB=BC，P为AB边上一点，连接CP，以PA、PC为邻边作□APCD，AC与PD相交于点E，已知∠ABC=∠AEP=α（0°<α<90°）.
（1）求证：∠EAP=∠EPA；
（2）□APCD是否为矩形？请说明理由；
（3）如图2，F为BC中点，连接FP，将∠AEP绕点E顺时针旋转适当的角度，得到∠MEN（点M、N分别是∠MEN的两边与BA、FP延长线的交点）.猜想线段EM与EN之间的数量关系，并证明你的结论.

已知：如图，四边形ABCD中AB=BC=1，CD=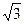，AD=1，
且∠B=90°。

试求：∠BAD的度数。
试求：四边形ABCD的面积（结果保留根号）

如图，折叠长方形一个角，点D落在BC边的点F处，BC=10㎝，AB=8㎝，求：求：FC的长度；
求：EF的长度.

正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.
在图1～图3中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：

正方形CEFG的边长	1	3	4
△BFD的面积

若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S_△BFD的大小，并结合图3证明你的猜想.