(本题9分)
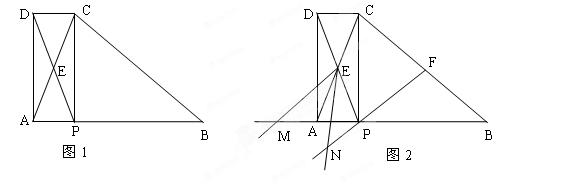
如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
相关知识点
推荐套卷

 (微克/毫升)与服药时间
(微克/毫升)与服药时间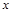 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当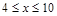 时,
时,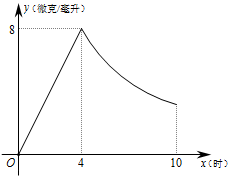

 轴对称的△A1B1C1;
轴对称的△A1B1C1;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号