（本小题满分6分）为了进一步了解义务教育阶段学生的体质健康状况，教育部对我市某中学九年级的部分学生进行了体质揣测．体质揣测的结果分为四个等级：优秀、良好、合格、不合格；根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息回答以下问题：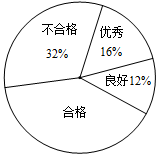
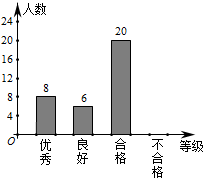
（1）在扇形统计图中，“合格“的百分比为 ．
（2）本次体质抽测中，抽测结果为“不合格“等级的学生有 人．
（3）若该校九年级有400名学生，估计该校九年级体质为“不合格“等级的学生约有 人．
相关试题
已知梯形ABCD中，AD∥BC，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连接DE．
（1）在下图中，用尺规作∠BAD的平分线AE（保留作图痕迹不写作法），并证明四边形ABED是菱形．
（2）若∠ABC=60°，EC=2BE．求证：ED⊥DC．
，把解集表示在数轴上，并求出不等式组的整数解．
，其中a2﹣4=0．如图，已知AB=AC，∠A=36°，AB的中垂线MD交AC于点D、交AB于点M．下列结论：
①BD是∠ABC的平分线；
②△BCD是等腰三角形；
③△ABC∽△BCD；
④△AMD≌△BCD．
正确的有（ ）个．
A、4 B、3 C、2 D、1
满分14分，第(1)小题4分，第(2)小题①6分、第(2)小题②4分）
（
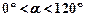且
，
边经过点B时，求旋转角
与AB所在直线交于点D，过点 D作DE∥
边于点E，联结BE.
时，设
，
，求
与
之间的函数解析式及定义域；
时，求
的长. 
相关知识点
推荐套卷
粤公网安备 44130202000953号