要对一块长60米、宽40米的矩形荒地
进行绿化和硬化．设计方案如图所示，矩形P、Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽都相等，并使两块绿地面积的和为矩形面积的
，求P、Q两块绿地周围的硬化路面的宽
如图，在平面直角坐标系中，四边形
为矩形，
，
，
为直线
上一动点，将直线
绕点逆时针方向旋转
交直线
于点
；
当点
在线段上运动（不与
重合）时，
求证：OA·BQ=AP·BP；在（1）成立的条件下，设点
的横坐标为
，
线段
的长度为
，求出关于的函数解析式，
并判断是否存在最小值，若存在，请求出最小值；
若不存在，请说明理由。直线
上是否存在点，使
为等腰三角形，若存在，
请求出点的坐标；若不存在，请说明理由。
有一个数学活动，其具体操作过程是：
第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开
（如图1）；
第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）.
请解答以下问题：如图2，若延长MN交线段BC于P，△BMP是什么三角形？请证明你的结论．
在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP
如图，在
ABCD的
各边AB、BC、CD、DA上，分别取点K、L、M、N，使A
K=CM、BL=DN，求证：四边形KLMN为平行四边形。
长方形ABCD中，DP平分∠ADC交BC于P点，将一个直角三角板的直角顶点放在P点处，并使它的一条直角边过A点，另一条直角边交CD于E点．
（1）找出图中与PA相等的线段．并说明理由．
（2）若点E为CD的三等分点，且BC=6，求BP的长.
如图，在矩形ABCD中，AB=3cm，AD=4cm，点E是BC上一动点（不与B、C重合），且DF⊥AE，垂足为F. 设AE=xcm，DF=ycm.
求证：△DFA∽△ABE；
试求y与x之间的函数关系式，并求出自变量的取值范围.
如图，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM=4，E为 BC边上的一个动点（不与B、C重合）．过E作直线AB的垂线，垂足为F． FE与DC的延长线相交于点G，连结DE，DF．.
求证：ΔBEF ∽ΔCEG．
当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．
设BE＝x，△DEF的面积为 y，请你求出y和x之间的函数关系式，并求出当x为何值时,y有最大值，最大值是多少？
将两个完全相同的长方形拼成如图所示的“L”形图案，判断△ACF是什么三角形？说明理由。
菱形ABCD的边长为5，两条对角线交于点O，且AO、BO的长分别是关于x的方程
两根，求m的值．
如图，P为正方形ABCD的对称中心，正方形ABCD的边长为
,
。直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以
个单位每秒速度运动，运动时间为t。求：
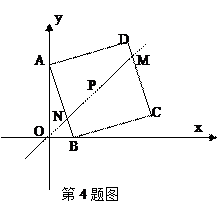
分别写出A、C、D、P的坐标；
当t为何值时，△ANO与△DMR相似？
△HCR面积S与t的函数关系式；并求以A、B、C、R为顶点的
四边形是梯形时t的值及S的最大值。
如图，在平面直角坐标系xoy中，矩型ABCD的边AB在x轴上，且AB=3，BC=
，直线y=
经过点C，交y轴于点G
点C、D的坐标分别是C（ ），D（ ）
求顶点在直线y=
上且经过点C、D的抛物线的解析式
将（2）中的抛物线沿直线y=
平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。
已知：如图所示，四边形ABCD是矩形，对角线AC，BD相交于点O，CE//DB，交AB的延长线于点E，AC与CE相等吗？请说明理由。
如图，四边形ABCD中，AB∥CD，AC平分∠BAD ，CE∥AD交AB于点E。
（1）判断：四边形AECD是什么形状？并给出理由。
（2）若点E是AB的中点，是判断△ABC的形状，并给出理由。
如图①，在等腰梯形ABCD中，AD∥BC，AB=CD，上底AD=2，梯形的高也等于2。一动点P从C出发，沿CB方向在线段BC上作匀速运动。
（1）若三角形ABP的面积S关于运动时间t的函数图象如图②所示，则可得BC长为 ； ；（4分。）
（2）在（1）的条件下，试求∠B的度数。（4分。）
图① 图②
粤公网安备 44130202000953号