初中数学圆内接四边形的性质解答题

王老师出了一道操作探究题：已知凸四边形ABCD（如甲图）纸片，能否将凸四边形纸片剪两刀，分割成四块，然后再拼成一个平行四边形？

小明思考一会儿后口述他的做法：（1）找出四边的中点E、F、G、H；（2）沿EG、FH剪两刀，分成四块；（3）在C点处（见乙图），将三块……说到这里，王老师打断了他的表述，“我只需要听到这里，你的思路及操作非常正确”.
（1）请你补充一下小明的口述，将Ⅰ、Ⅱ、Ⅲ进行怎样的变换与Ⅳ拼在一起？
（2）请你说明一下，乙图是平行四边形纸块吗？（将两个图形进行恰当标注，以便解决问题）

已知E、F分别是平行四边形ABCD的边AB、CD的中点，BD是对角线，AG∥BD交CB的延长线于G.

（1）试说明△ADE≌△CBF；
（2）当四边形AGBD是矩形时，请你确定四边形BEDF的形状并说明；
（3）当四边形AGBD是矩形时，四边形AGCD是等腰梯形吗？直接说出结论.

(本小题6分) 如图，在梯形中，，，，，，求的长．

如图1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．
求证：ME = MF．
如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．
如图3，若将原题中的“正方形”改为“矩形”，且AB = mBC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．
根据前面的探索和图4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由

如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，
操作示例
我们可以取直角梯形ABCD的一腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC拼接到△PFD的位置，构成新的图形（如图2）．
思考发现
小明在操作后发现，该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置，易知PE与PF在同一条直线上．又因为在梯形ABCD中，AD∥BC，∠C+∠ADP=180°，则∠FDP+∠ADP=180°，所以AD和DF在同一条直线上，那么构成的新图形是一个四边形，进而根据平行四边形的判定方法，可以判断出四边形ABEF是一个平行四边形，而且还是一个特殊的平行四边形——矩形．
图2中，矩形ABEF的面积是               ；（用含a，b，c的式子表示）

类比图2的剪拼方法，请你就图3(其中AD∥BC)和图4（其中AB∥DC）的两种情形分别画出剪拼成一个平行四边形的示意图．

小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．
如图5的多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一个平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

如图，等腰△OBD中，OD=BD，△OBD绕点O逆时针旋转
一定角度后得到△OAC，此时正好B、D、C在同一直线上，
且点D是BC的中点.

求△OBD旋转的角度
求证：四边形ODAC是菱形.

如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：∠BAE＝∠DCF。

如图1,在△ABC中，∠ACB=90°，∠CAB=30°,△ABD是等边三角形，
E是AB的中点，连结CE并延长交AD于F.
求证：① △AEF≌△BEC；
② 四边形BCFD是平行四边形；
如图2，将四边形ACBD折叠,使D与C重合，HK为折痕，求sin∠ACH的值.

在平面直角坐标系中，把矩形OABC的边OA、OC
分别放在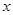轴和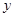轴的正半轴上，已知OA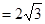，OC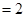


直接写出A、B、C三点的坐标
将矩形OABC绕点O逆时针旋转°，得到矩形OA₁B₁C₁，
其中点A的对应点为点A₁．
①当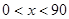时，设AC交OA₁于点K（如图1），
若△OAK为等腰三角形，请直接写出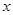的值；
②当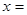90时（如图2），延长AC交A₁C₁于点D，
求证：AD⊥A₁C₁；
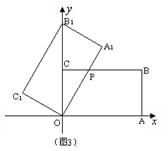
③当点B₁落在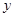轴正半轴上时（如图3），设BC
与OA₁交于点P，求过点P的反比例函数的解析式；
并探索：该反比例函数的图象是否经过矩形OABC
的对称中心？请说明理由．

如图，已知平行四边形ABCD的对角线AC的垂直
平分线与边AD、BC分别交于E、F两点，垂足是点O．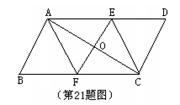

求证：△AOE≌△COF；
问：四边形AFCE是什么特殊的四边形？
（直接写出结论，不需要证明）

(本题8分)已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

（1）求证：EG=CG；
（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．
（3）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．     
（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（本小问均不要求证明）

(本题6分) 已知：如图，在△ABC中， D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF＝DC,连结CF．

（1）求证：D是BC的中点；
（2）如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．

在四边形ABCD中，AB=BC，BF平分∠ABC，AF∥DC，
连接AC，CF. 求证：（1）AF=CF；（2）CA平分∠DCF.

(本题满分10分)
如图，F为正方形ABCD的对角线AC上一点，FE⊥AD于点E，M为CF的中点．

（1）求证：MB=MD；
（2）求证：ME=MB．

(本题满分12分)在四边形ABCD中，AD＝a，CD＝b，点E在射线BA上，点F在射线BC上．

观察计算：
(1)如图①，若四边形ABCD是矩形，E是AB的中点．F是BC的中点，则四边形DEBF   的面积S四边形DEBF＝_______．
(2)若四边形ABCD是平行四边形，E是AB的中点，F是BC的中点，则S四边形DEBF：S四边形ABCD＝_______．
(3)如图②，若四边形ABCD是平行四边形，且BE：AB＝2：3，BF：BC＝2：3，则S四边形DEBF：S四边形ABCD＝_______．
探索规律：
如图③，在四边形ABCD中，若BE：AB＝n：m，BF：BC＝n：m，试猜想S四边形DEBF：S四边形ABCD＝_______，请说明理由．
　解决问题：
　如图④，某小区角落有一四边形空地，为了充分利用空间，美化环境，想把它沿两侧墙壁改造为一块绿地，使绿地面积是原空地面积的3倍．请分别在两侧墙壁上确定点E、F，画出改造线DE、DF，并写出作法．