[江苏]2011—2012学年无锡市第一学期期中考试九年级数学试卷
甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均
数都是8环,甲的方差是1.2,乙的方差是1.8.下列说法中不一定正确的是
| A.甲、乙的众数相同 | B.甲的成绩稳定【】 |
| C.乙的成绩波动较大 | D.甲、乙射中的总环数相同 |
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是 m(可利用的围墙长度超过6m).
如图,在平面直角坐标系中,将线段OC向右平移到AB,且OA=OC,所得菱形OABC 的顶点 的坐标是(3,4),则顶点
的坐标是(3,4),则顶点 、
、 的坐标分别是_________________.
的坐标分别是_________________.
如图,在□ABCD中,点E在边AD上,以BE为折痕将△ABE向上翻折,点A正好落在CD的点F处,若△FDE的周长为8,△FCB的周长为22,则YABCD的周长为 .
为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山 上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?

 ,得
,得 则 【 】
则 【 】




 的常数项为0,则m的值等于
的常数项为0,则m的值等于  【 】
【 】

 .
.
 =0,那么x3-y3 = .
=0,那么x3-y3 = . 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 . ,则梯形ABCD的面积为 cm2.
,则梯形ABCD的面积为 cm2.
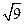 +|-2|+
+|-2|+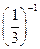 +(-1)2011
+(-1)2011
 (用配方法)
(用配方法) 
 等边三角形.
等边三角形.
 有两个不相等的实数根.
有两个不相等的实数根.

 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?
 C的周长是否也被射线QN平分.
C的周长是否也被射线QN平分.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号