[四川]2011-2012年四川省成都铁中八年级上学期期中检测数学卷
下列哪组数能作为直角三角形的三边长( )
| A.9,12,15 | B.4,4,8 | C. |
D.12,35,36 |
下列说法中,正确的是( )
| A.对角线相等的四边形是矩形 |
| B.对角线互相垂直的四边形是菱形 |
| C.对角线相等的平行四边形是矩形 |
| D.对角线互相垂直的平行四边形是矩形 |
若菱形的两条对角线长分别为6和8, 则这个菱形的周长为( )
| A.20 | B.16 | C.12  |
D.10 |
已知一个多边形的内角和与外角和的比是2∶1,则它的边数为( )
| A.9 | B.8 | C.7 | D.6 |
在:等边三角形、平行四边形、正方形、菱形和等腰梯形四种图形中,是中心对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为( )

| A.30° | B.35° | C.40 ° ° |
D.50° |
已知四边形ABCD,有
①AB∥CD;②AB=CD;③BC∥AD;④BC="AD." 从这四个条件中任选两个, 能使四边形ABCD成为平行四边形的选法种数,共有( )
A.3种 B.4种 C.5种 D.6种
如图,已知等腰△ABC,AC="BC=5cm," AB="6cm," 则等腰△ABC的面积是 cm2.
如图,在□ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为 .
操作题
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上),在给出的方格纸中,按下列要求改变位置作出相应的图形
(1)向右平移10格,再向下平移1格得到四边形EFGH;
(2) 绕点C沿顺时针旋转90°得到四边形A1B1CD1;
绕点C沿顺时针旋转90°得到四边形A1B1CD1;
(3)若小方格的边长为1,试计算四边形ABCD的周长和面积.
(8分)如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
(10分)如图,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图,连接AE和GC. 你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
如图,在△ABC中,AD⊥BC于D,若AC=13,AD=12,
△ABC的面积为126,则AB= .
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将梯形的腰CD以点D为中心逆时针旋转90°至DE,连接AE,CE,若△ADE的面积为3,那么BC的长为 ..
(8分) 观察下列各式及验证过程: . 验证:
. 验证: 
 . 验证:
. 验证: 
 . 验证:
. 验证: 
(1)按照上述三 个等式及其验证过程的基本思路,猜想
个等式及其验证过程的基本思路,猜想 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n 的自然数)表示的等式,并进行验证.
的自然数)表示的等式,并进行验证.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
 的算术平方根是( )
的算术平方根是( )



 ,
, 的大小,正确的是( )
的大小,正确的是( ) 有意义,则x的取值范围 是 .
有意义,则x的取值范围 是 . (相邻两个5之间的“0”的个数逐次增加1), 其中无理数有 个.
(相邻两个5之间的“0”的个数逐次增加1), 其中无理数有 个. = ;
= ; = .
= .
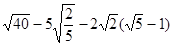

 ,求
,求 的值
的值 ,
, ,则
,则 的值为 .
的值为 . 的平方根是
的平方根是 3,则m= ..
3,则m= .. G的边长
G的边长
 粤公网安备 44130202000953号
粤公网安备 44130202000953号