如图1所示,已知在△ABD和△AEC中,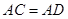 ,
,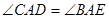 ,
,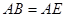
如图1,试说明:
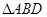 ≌
≌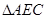 ;
;如图1,若
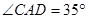 ,
,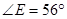 ,
,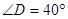 ,
,
①试求: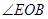 的度数
的度数
②将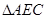 绕点A逆时针旋转
绕点A逆时针旋转 度(
度(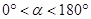 ),问当
),问当 为多少度时,直线CE分别与
为多少度时,直线CE分别与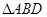 的三边所在的直线垂直?(请直接写出答案)。
的三边所在的直线垂直?(请直接写出答案)。如图2将
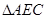 绕点A逆时针旋转后得到
绕点A逆时针旋转后得到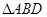 ,并使点D,E,A三点在同一条直线上,若
,并使点D,E,A三点在同一条直线上,若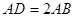 ,连接CD,若
,连接CD,若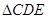 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。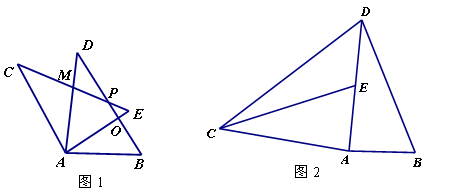
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.

(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数是否总保持不变,
若∠FCN的大小保持不变,请说明理由;
若∠FCN的大小发生改变,请举例说明;
如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算蔬菜的产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.请你和小明一起来求这块土地的面积.
 |
已知△ABC中,∠ACB=90°,AC=6,BC=8,过点A作直线MN⊥AC,点P是直线MN上的一个动点(与点A不重合),连结CP交AB于点D,设AP= ,AD=
,AD= .
.如图1,若点P在射线AM上,求y与x的函数解析式;

射线AM上是否存在一点P,使以点D、A、P组成的三角形与△ABC相似,若存在,求AP的长,若不存在,说明理由;
如图2,过点B作BE⊥MN,垂足为E,以C为圆心、AC为半径的⊙C与以P为圆心PD为半径的动⊙P相切,求⊙P的半径

如图4,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB= ,BC=26.
,BC=26.
求:
cos∠DAC的值;
线段AD的长
如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
求证:OE=OF
如图2,若点E在AC的延长线上,AM
 BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由
BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=________.
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.
①请在图1中补全小贝同学翻折后的图形;
②m的取值范围是____________.
宽与长的比是 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形 ;
;
第二步:分别取 ,
, 的中点
的中点 ,
, ,连接
,连接 ;
;
第三步:以 为圆心,
为圆心, 长为半径画弧,交
长为半径画弧,交 的延长线于
的延长线于 ;
;
第四步:过 作
作 ⊥
⊥ ,交
,交 的延长线于
的延长线于 。
。
请你根据以上作法,证明矩形 为黄金矩形。
为黄金矩形。
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系是
如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .

如图,在直角梯形ABCD中,∠D =∠BCD = 90°,∠B = 60°,AB = 6,AD = 9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G,如图①.

求CD的长及∠1的度数;
设DE = x,△GEF与梯形ABCD重叠部分的面积为y.
 求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移,速度为每秒1个单位,当E点移动到线段AB上时运动停止.设平移时间为t(秒),在平移过程中是否存在某一时刻t,使得△ABE为等腰三角形?若存在,求出t的值;若不存在,请说明理由
如图,四边形ABCD为菱形,已知A(0,6),D(-8,0).
求点C的坐标
设菱形ABCD对角线AC、BD相交于点E,求经过点E的反比例函数解析式.
已知线段 ,
, .
.
(1)已知线段 垂直于线段
垂直于线段 .设图(1)、图(2)和图(3)中的四边形
.设图(1)、图(2)和图(3)中的四边形 的
的
面积分别为 ,
, 和
和 ,则
,则 = ,
= , = ,
= , = ;
= ;
(2)如图(4),对于线段 与线段
与线段 垂直相交(垂足
垂直相交(垂足 不与点
不与点 ,
, ,
, ,
, 重合)的任意情形,请你就四边形
重合)的任意情形,请你就四边形 面积的大小提出猜想,并证明你的猜想.
面积的大小提出猜想,并证明你的猜想.
如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.若动点M、N同时出发,经过几秒钟两点相遇?
若点E在线段BC上,BE=2cm,动点M、N同时出发且相遇时均停止运动,那么点M运动到第几秒钟时,与点A、E、N恰好能组成平行四边形?

(本题6分)
如图,梯形ABCD中, DC∥AB,点E是BC的中点,连结AE并延长与DC的延长线相交于点F,连结BF,AC.
求证:四边形ABFC是平行四边形;