初中数学圆内接四边形的性质解答题

已知：如图，在直角梯形ABCD中，AD // BC，AB⊥AD，BC = CD，BE⊥CD，垂足为点E，点F在BD上，联结AF、EF．

求证：AD = ED；
如果AF // CD，求证：四边形ADEF是菱形

如图，△ABC和△ADC都是边长相等的等边三角形，点E、F同时分别从点B、 A出发，各自沿BA、AD方向运动到点A、D停止，运动的速度相同，连接EC、FC．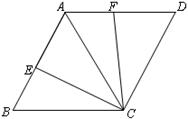

（1）写出在点E、F运动过程中，所有全等的三角形。
（2）点E、F运动过程中∠ECF的大小是否随之变化？请说明理由；
（3）点E、F运动过程中，以点A、E、C、F为顶点的四边形的面积变化吗？请说明理由;
（4）接EF，在图中找出和∠ACE相等的所有角，并说明理由．

如图，在平行四边形ABCD中，点P是对角线AC上的一点，PE⊥AB，PF⊥AD，垂足分别为E、F，且PE=PF，平行四边形ABCD是菱形吗？为什么？

如图，将边长为3cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD的中点 M处，点C落在点N处，MN与CD交于点P， 连接EP．

(1) △AEM的周长=_____cm；（2）求证：EP=AE+DP；

已知：如图，△ABC中，AD是BC边上的中线，四边形ABDE是平行四边形
（1）求证：四边形ADCE是平行四边形；
（2）当△ABC满足什么条件时，四边形ADCE是菱形？说明你的理由.

已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

（1）求证：EG=CG；
（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．
正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

（3）若将（1）中的“正方形ABCD”改为“正边形ABCD…X”，请你作出猜想：当∠AMN=        °时，结论AM=MN仍然成立．
（直接写出答案，不需要证明）

如图，在梯形ABCD中，AD∥BC，∠DCB＝45°，CD ＝2，BD⊥CD ．过点C作CE⊥AB于E，交对角线BD于F．点G为BC中点，连结EG、AF．
求EG的长
求证：CF ＝AB ＋AF

在Rt△ABC中，∠BAC=90°，∠B=30°，线段AD是BC边上的中线．
如图(Ⅰ)，将△ADC沿直线BC平移，使点D与点C重合，得到△FCE，连结AF．求证：四边形ADEF是等腰梯形；

如图(Ⅱ)，在（1）的条件下，再将△FCE绕点C顺时针旋转，设旋转角为（0°<<90°）连结AF、DE．

AC⊥CF时，求旋转角的度数；②当=60°时，请判断四边形ADEF的形状，并给予证明．

如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在边OA的点D处．已知折痕CE＝5，且．
判断△OCD与△ADE是否相似？请说明理由；
求直线CE与x轴交点P的坐标；
是否存在过点D的直线l，使直线l、直线CE与x轴所围成的三角形和直线l、直线CE与y轴所围成的三角形相似？如果存在，请直接写出其解析式并画出相应的直线；如果不存在，请说明理由．

如图，□ABCD中，AB＝4，BC＝3，∠BAD＝120°，动点E在BC上（不与B
重合）．作EF⊥AB于F，FE、DC的延长线交于点G．设BE＝x，△DEF的面积为S．
求S关于x的函数表达式，并写出x的取值范围
当点E在何处时，S有最大值，最大值为多少？

如图，矩形ABCD中，AD∥BC，AB＝4cm，BC＝8cm，动点M从点D出发，按折线DCBAD方向以2cm/s的速度运动，动点N从点D出发，按折线DABCD方向以1cm/s的速度运动．
（1）若动点M、N同时出发，经过几秒钟两点相遇？
（2）若点E在线段BC上，且BE＝3cm，若动点M、N同时出发，相遇时停止运动，经过几秒钟，点A、E、M、N组成平行四边形？

如图，用同样规格的花色和白色两种正方形地砖铺设矩形地面，请观察图形并解答有关问题：（1）有第n个图形中，白色地砖总块数为           块
（2）在第n个图形中，花色地砖总块数为           块
（3）是否存在白色地砖与花色地砖数量相等的情形？若存在求出n的值，若不存在说明理由。

如图，在梯形ABCD中，AD∥BC，∠B=90°,AD=18cm，BC=21cm，点P从点A开始沿AD边向D以1cm/s的速度移动，点Q从点C开始沿CB边向B以2cm/s的速度移动，如果P、Q分别从A、C同时出发，设移动的时间为t(s)，求：

（1）t为何值时，四边形PQCD为平行四边形；
（2）t为何值时，四边形ABQP为矩形；
（3）t为何值时，梯形PQCD是等腰梯形。

已知等腰三角形ABC中，AB=AC，AD平分∠BAC交于BC于 D点，在AD上任取一点P，（A点除外），过P点作EF∥AB，分别交AC、BC于点E、F，作PM∥AC，交AB于点M，连结ME。
（1）求证：四边形AEPM为菱形；
（2）当P点在何处时，菱形AEPM的面积为四边形EFBM面积的一半。