[广东]2012届广东汕头澄海区中考模拟数学试卷
如图,已知AD、BC分别是⊙O的两条弦,AD∥BC,∠AOC=80°,则∠DAB的度数为
A.40° B.50° C.60° D.80°
如图,函数 与
与 的图象交于A、B两点,过点A作AC垂直于
的图象交于A、B两点,过点A作AC垂直于 轴,垂足为C,则△BOC的面积为
轴,垂足为C,则△BOC的面积为
A.8 B.6 C.4 D.2
据汕头统计网消息,在全国第六次人口普查中显示,我市常住人口总数为5391028人,将这个总人口数(保留两个有效数字)用科学记数法表示为 .
如图,光源P在横杆AB的上方,AB在灯光下的影子为CD,AB∥CD,若PA=2cm,PC="6" cm ,AB=3cm,那么CD=_______ cm.
如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为 . 
某校对九年级学生进行了一次数学学业水平测试,成绩评定分为A、B、C、D四个等级(注:等级A、B、C、D分别代表优秀、良好、合格、不合格),学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析,并绘制成扇形统计图(如图所示).
根据图中所给的信息回答下列问题:
随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?
这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?
若该校九年级学生有800名,请你估计这次数学学业水平测试中,
成绩达合格以上(含合格)的人数大约有多少人?
在边长为1的正方形网格中,有△ABC和半径为2的⊙P.
以点M为位似中心,在网格中将△ABC放大2倍得到△A´B´C´,请画出△A´B´C´;

在(1)所画的图形中,求线段AB的对应线段A´B´被⊙P所截得的弦DE的长.
如图,在某海域内有三个港口P、M、N.港口M在港口P的南偏东60°的方向上,港口N在港口M的正西方向上,P、M两港口相距20海里,P、N两港口相距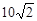 海里.求:
海里.求: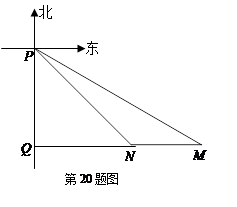
港口N在港口P的什么方向上?请说明理由
M、N两港口的距离(结果保留根号).
若 a是不为1的有理数,我们把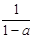 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是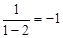 ,
,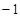 的差倒数是
的差倒数是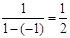 .已知
.已知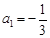 ,
,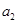 是
是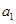 的差倒数,
的差倒数,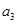 是
是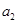 的差倒数,
的差倒数,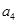 是
是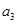 的差倒数,…,依此类推.
的差倒数,…,依此类推.分别求出
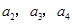 的值
的值求
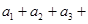 ……
……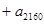 的值
的值
今年“五一”期间,某旅游公司对某条旅游线路推出如下套餐:如果出团人数不超过25人,人均费用500元;如果出团人数超过25人,每增加1人,人均费用降低10元,但人均费用不得低于400元.某单位组织一批员工到该线路参观旅游,如果人均费用想要低于500元,但不低于420元,那么参观旅游的人数在什么范围内?请通过计算说明
若该单位已付旅游费用13500元,求该单位安排了多少名员工去参观旅游.
在Rt△ABC中,∠BAC=90°,∠B=30°,线段AD是BC边上的中线.如图(Ⅰ),将△ADC沿直线BC平移,使点D与点C重合,得到△FCE,连结AF.求证:四边形ADEF是等腰梯形;

如图(Ⅱ),在(1)的条件下,再将△FCE绕点C顺时针旋转,设旋转角为
 (0°<
(0°< <90°)连结AF、DE.
<90°)连结AF、DE.
AC⊥CF时,求旋转角 的度数;②当
的度数;②当 =60°时,请判断四边形ADEF的形状,并给予证明.
=60°时,请判断四边形ADEF的形状,并给予证明.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
求抛物线对应的函数关系式;
若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由
在(2)的条件下,连结BD,已知在对称轴上存在一点P,使得△PBD的周长最小.请求出点P的坐标.
在(2)、(3)的条件下,若点M是线段OB上的一个动点(与点O、B不重合),过点M作MN∥BD交x轴于点N,连结PM、PN,设OM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在最大值?若存在,求出最大值并求此时M点的坐标;若不存在,请说明理由.


 的自变量
的自变量 的取值范围是
的取值范围是







 因式分解的结果是
因式分解的结果是




 ☆
☆
 ,根据这个规则,计算2☆3的值是
,根据这个规则,计算2☆3的值是


 的相反数是2,
的相反数是2, ,则
,则 的值为____________.
的值为____________. .
.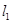 :
: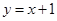 与直线
与直线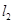 :
: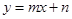 相交于点
相交于点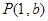 .
.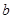 的值
的值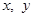 的方程组
的方程组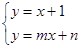 ,请你直接写出它的解;
,请你直接写出它的解;
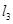 :
: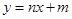 是否也经过点
是否也经过点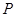 ?请说明理由
?请说明理由 ,其中
,其中 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号