如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
求抛物线对应的函数关系式;
若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由
在(2)的条件下,连结BD,已知在对称轴上存在一点P,使得△PBD的周长最小.请求出点P的坐标.
在(2)、(3)的条件下,若点M是线段OB上的一个动点(与点O、B不重合),过点M作MN∥BD交x轴于点N,连结PM、PN,设OM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在最大值?若存在,求出最大值并求此时M点的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
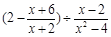 ,其中
,其中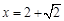 ;
;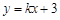 (
(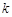 <0)分别交
<0)分别交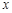 轴、
轴、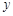 轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作
轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作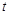 秒.
秒.
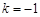 时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).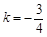 时,设以C为顶点的抛物线
时,设以C为顶点的抛物线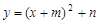 与直线AB的另一交点为D
与直线AB的另一交点为D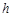 ,当
,当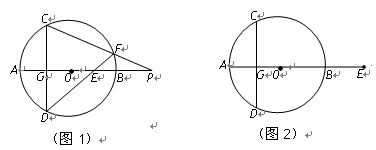
 只福娃的成本为
只福娃的成本为 (元),每只售价
(元),每只售价 (元),且
(元),且 ,
, .当日产量为多少时,可获得最大利润?最大利润是多少?
.当日产量为多少时,可获得最大利润?最大利润是多少? ),点B的坐标为(-6,0).
),点B的坐标为(-6,0).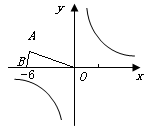
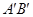 ,请直接写出A、B的对称点
,请直接写出A、B的对称点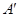
 的坐标;
的坐标; 沿x轴向右平移a个单位,此时点A恰好落在反比例函数
沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图像上,求a的值.
的图像上,求a的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号