如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.求NC,MC的长(用t的代数式表示)
当t为何值时,四边形PCDQ构成平行四边形?
当t为何值时,射线QN恰好将△ABC的面积平分?并判断此时△ABC的周长是否也被射线QN平分.

在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED求证:△BEC≌△DEC;
延长BE交AD于F,当∠BED=120°时,求
 的度数.
的度数.
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,点P、Q分别是边AD和AE上的动点(两动点都不与端点重合).
(1)PQ+DQ的最小值是 ;
(2)说出PQ+DQ取得最小值时,点P、点Q的位置,并在图8中画出;
(3)请对(2)中你所给的结论进行证明.
如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足, AC=BC. 
⑴求证:CD=BE.⑵若AD=3,DC=4,求AE.
如图,在矩形ABCD中,
请完成如下操作:①作
 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);请在(1)的基础上,完成下列问题:
①判断直线BC与圆 的位置关系,并说明理由;
的位置关系,并说明理由;
②若圆 与AC边的另一个交点为F,
与AC边的另一个交点为F,
 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
已知:如图,正比例函数 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点

试确定上述正比例函数和反比例函数的表达式;
根据图象直接回答,在第一象限内,当
 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值? 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中 ,过点
,过点 作直线
作直线 轴,交
轴,交 轴于点
轴于点 ;过点
;过点 作直线
作直线 轴交
轴交 轴于点
轴于点 ,交直线
,交直线 于点
于点 .当四边形
.当四边形 的面积为6时,请判断线段
的面积为6时,请判断线段 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.

已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由
如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比
如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

已知:如图,在平行四边形ABCD中,AE是BC边上的高,将 沿
沿 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得 .
.求证:
 ;
;若
 ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论.
已知两个全等的直角三角形纸片ABC、DEF,如图⑴放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.求证:△EGB是等腰三角形
若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图⑵).求此梯形的高

如图,在四边形ABCD中, ∥
∥ ,
, ,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为
,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为 。
。
求CD的长;
当四边形PBQD为平行四边形时,求四边形PBQD的周长;
在点P、点Q的运动过程中,是否存在某一时刻,使得
 的面积为20
的面积为20 ,若存在,请求出所有满足条件的
,若存在,请求出所有满足条件的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
在直角梯形ABCD中,AB∥CD,∠ABC=900,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA、OB的中点分别为点E、F求证:

求
 的值
的值若直线EF与线段AD、BC分别相交于点G、H,求
 的值
的值
如图1,将正方形纸片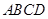 折叠,使点
折叠,使点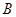 落在
落在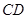 边上一点
边上一点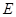 (不与点
(不与点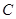 ,
,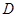 重合),压平后得到折痕
重合),压平后得到折痕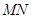 .
.
当
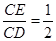 时,求
时,求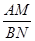 的值.(方法指导:为了求得
的值.(方法指导:为了求得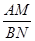 的值,可先求
的值,可先求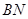 、
、 的长,不妨设
的长,不妨设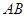 =2)
=2)在图1中,若
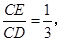 则
则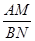 的值等于 ;若
的值等于 ;若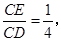 则
则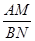 的值等于 ;若
的值等于 ;若 (
(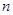 为整数),则
为整数),则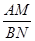 的值等于 .(用含
的值等于 .(用含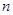 的式子表示)
的式子表示)如图2,将矩形纸片
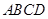 折叠,使点
折叠,使点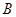 落在
落在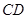 边上一点
边上一点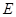 (不与点
(不与点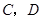 重合),压平后得到折痕
重合),压平后得到折痕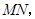 设
设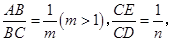 则
则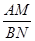 的值等于 .(用含
的值等于 .(用含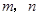 的式子表示)
的式子表示)