[广东]2012届广东省广州市白云区中考一模数学卷
已知两条线段的长度分别为2cm、8cm,下列能与它们构成三角形的线段长度为(*)
| A.4cm | B.6cm | C.8cm | D.10cm |
如图,⊙O是△ABC的外接圆,∠A=50°,则∠OBC的度数等于(*)
| A.50° | B.40° | C.45° | D.100° |
如图,梯形ABCD中,AD∥BC,AC、BD交于点O,AD=1,BC=3,
则S△AOD︰S△BOC等于(*)
(A)1︰2 (B)1︰3 (C)4︰9 (D)1︰9
若一次函数 =
= +
+ ,当
,当 的值增大1时,
的值增大1时, 值减小3,则当
值减小3,则当 的值减小3时,
的值减小3时, 值(*)
值(*)
| A.增大3 | B.减小3 | C.增大9 ( | D.减小9 |
在一次数学测验中,某学习小组的六位同学的分数分别是54,85,92,73,61,85.这组数据的平均数是 * ,众数是 * ,中位数是 * .
如图, 是以边长为6的等边△ABC一边AB为半径的四分之一圆周,P为
是以边长为6的等边△ABC一边AB为半径的四分之一圆周,P为 上一动点.当BP经过弦AD的中点E时,四边形ACBE的周长为 * (结果用根号表示).
上一动点.当BP经过弦AD的中点E时,四边形ACBE的周长为 * (结果用根号表示).
如图,等腰△OAB的顶角∠AOB=30°,点B在 轴上,腰OA=4.
轴上,腰OA=4.
(1)B点的坐标为: ;
(2)画出△OAB关于 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
(3)求出经过A1点的反比例函数解析式.
(注:若涉及无理数,请用根号表示)
在-2,-3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点的个数为 ;
(2)求过P点的正比例函数图象经过第二、四象限的概率(用树形图或列表法求解);
(3)过点P的正比例函数中,函数 随自变量
随自变量 的增大而增大的概率为 .
的增大而增大的概率为 .
在同一间中学就读的李浩与王真是两邻居,平时他们一起骑自行车上学.清明节后的一天,李浩因有事,比王真迟了10分钟出发,为了能赶上王真,李浩用了王真速度的1.2倍骑车追赶,结果他们在学校大门处相遇.已知他们家离学校大门处的骑车距离为15千米.求王真的速度.
如图,已知⊙O的弦AB等于半径,连结OB并延长使BC=OB.
(1)∠ABC= °;
(2)AC与⊙O有什么关系?请证明你的结论;
(3)在⊙O上,是否存在点D,使得AD=AC?若存在,请画出图形,并给出证明;若不存在,请说明理由.
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,点P、Q分别是边AD和AE上的动点(两动点都不与端点重合).
(1)PQ+DQ的最小值是 ;
(2)说出PQ+DQ取得最小值时,点P、点Q的位置,并在图8中画出;
(3)请对(2)中你所给的结论进行证明.
 的系数为(*)
的系数为(*) 的解集是(*)
的解集是(*) 3
3 <3
<3




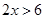 的解集为 * .
的解集为 * .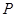 (-2,1)关于原点对称的点
(-2,1)关于原点对称的点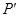 的坐标为 * .
的坐标为 * . 的结果为 * .
的结果为 * . .
.
 ,其中
,其中 =-
=- .
. =
= +
+ +
+ -4.
-4. =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标; 轴有交点,且经过
轴有交点,且经过 粤公网安备 44130202000953号
粤公网安备 44130202000953号