如图,等腰△OAB的顶角∠AOB=30°,点B在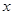 轴上,腰OA=4.
轴上,腰OA=4.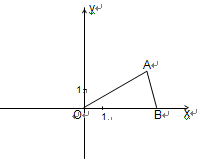
(1)B点的坐标为: ;
(2)画出△OAB关于 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
(3)求出经过A1点的反比例函数解析式.
(注:若涉及无理数,请用根号表示)
相关知识点
推荐套卷
如图,等腰△OAB的顶角∠AOB=30°,点B在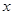 轴上,腰OA=4.
轴上,腰OA=4.
(1)B点的坐标为: ;
(2)画出△OAB关于 轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
(3)求出经过A1点的反比例函数解析式.
(注:若涉及无理数,请用根号表示)