如图，正方形ＡＢＣＤ的边长是４，∠ＤＡＣ的平分线交ＤＣ于点Ｅ，点Ｐ、Ｑ分别是边ＡＤ和ＡＥ上的动点（两动点都不与端点重合）．
（１）ＰＱ＋ＤＱ的最小值是 ；
（２）说出ＰＱ＋ＤＱ取得最小值时，点Ｐ、点Ｑ的位置，并在图８中画出；
（３）请对（２）中你所给的结论进行证明．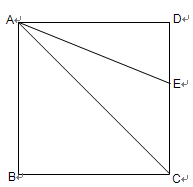
（
）与行驶时间
（
）之间的函数图象．
（1）求甲车行驶过程中相关知识点
推荐套卷
如图，正方形ＡＢＣＤ的边长是４，∠ＤＡＣ的平分线交ＤＣ于点Ｅ，点Ｐ、Ｑ分别是边ＡＤ和ＡＥ上的动点（两动点都不与端点重合）．
（１）ＰＱ＋ＤＱ的最小值是 ；
（２）说出ＰＱ＋ＤＱ取得最小值时，点Ｐ、点Ｑ的位置，并在图８中画出；
（３）请对（２）中你所给的结论进行证明．
粤公网安备 44130202000953号