在-2,-3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点的个数为 ;
(2)求过P点的正比例函数图象经过第二、四象限的概率(用树形图或列表法求解);
(3)过点P的正比例函数中,函数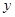 随自变量
随自变量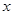 的增大而增大的概率为 .
的增大而增大的概率为 .
相关知识点
推荐套卷
在-2,-3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点的个数为 ;
(2)求过P点的正比例函数图象经过第二、四象限的概率(用树形图或列表法求解);
(3)过点P的正比例函数中,函数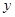 随自变量
随自变量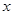 的增大而增大的概率为 .
的增大而增大的概率为 .