如图,已知E,F分别是平行四边形ABCD的边AD、BC上的点,且AE= AD,CF=
AD,CF= BC.求证:四边形AECF是平行四边形.
BC.求证:四边形AECF是平行四边形.
如图,▱ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.求证:△GAB是等腰三角形.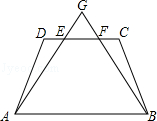
如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现了什么?请写出一条.
图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.


(1)画一个底边为4,面积为8的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个面积为12的平行四边形。
如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)图②中阴影部分的正方形的边长是 _________ ;
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: _________ ;
方法2: _________ ;
(3)观察图②,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 _________ ;
(4)根据(3)中的等量关系解决如下问题:若m﹣n=﹣5,mn=3,则(m+n)2的值为多少?
如图,请在下列三个关系中,选出两个恰当的关系作为条件,填在已知条件的横线上,推出四边形ABCD是平行四边形,并予以证明。
关系:①AD∥BC,②AB=CD,③∠A=∠C。
已知:在四边形ABCD中, , .
求证:四边形ABCD是平行四边形.
在 ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC= 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.
如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.
(1)证明:AF∥HG(图(1));
(2)如果点C的对应点H恰好落在边AD上(图(2)).判断四边形AECH的形状,并说明理由.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.