图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.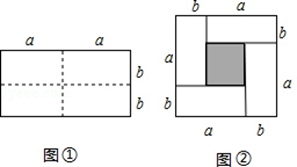
(1)图②中阴影部分的正方形的边长是 _________ ;
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: _________ ;
方法2: _________ ;
(3)观察图②,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 _________ ;
(4)根据(3)中的等量关系解决如下问题:若m﹣n=﹣5,mn=3,则(m+n)2的值为多少?
相关知识点
推荐套卷
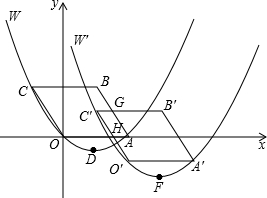
 OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和
OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和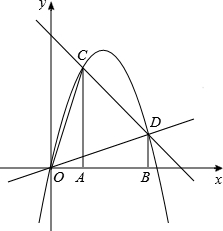
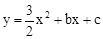 的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.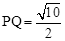 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.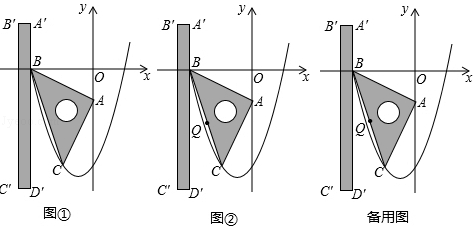
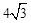 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题: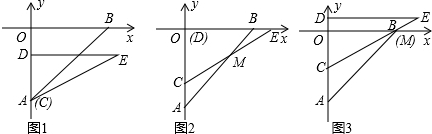
 粤公网安备 44130202000953号
粤公网安备 44130202000953号