如图,已知 ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.
ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.
如图,BD是菱形ABCD的对角线,点E、F分别在边CD、DA上,且CE=AF.
求证:BE=BF.
如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.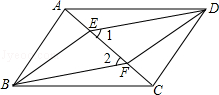
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
如图,在 ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC.
(1)求证:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)四边形ABEC一定是什么四边形?
(2)证明你在(1)中所得出的结论.
如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.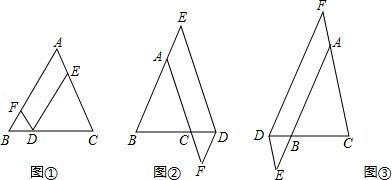
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
在△ABC中,AB=AC,点D、E、F分别是AC、BC、BA延长线上的点,四边形ADEF为平行四边形.求证:AD=BF.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
求证:OE=BC.
已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.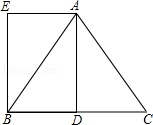
如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.
求证:AE∥CF.