如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.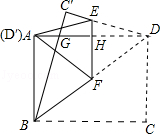
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
推荐套卷
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.