初中数学圆内接四边形的性质试题

已知：平行四边形ABCD中，过对角线AC中点O的直线EF交AD于F，BC于E。
求证：BE=DF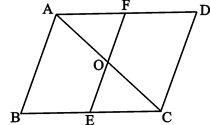

如图，在Rt△ABC中，∠C=90°，AC=6，BC=8．动点P从点A开始沿折线AC-CB-BA运动，点P在AC，CB，BA边上运动的速度分别为每秒3，4，5 个单位．直线l从与AC重合的位置开始，以每秒个单位的速度沿CB方向平行移动，即移动过程中保持l∥AC，且分别与CB，AB边交于E，F两点，点P与直线l同时出发，设运动的时间为t秒，当点P第一次回到点A时，点P和直线l同时停止运动

（1）①当t=3秒时，点P走过的路径长为       ；②当t=          秒时，点P与点E重合；③当t=     秒时，PE∥AB；
（2）当点P在AC边上运动时，将△PEF绕点E逆时针旋转，使得点P的对应点M落在EF上，点F的对应点记为点N，当EN⊥AB时，求t的值；
（3）当点P在折线AC-CB-BA上运动时，作点P关于直线EF的对称点，记为点Q．在点P与直线l运动的过程中，若形成的四边形PEQF为菱形，请直接写出t的值．

如图，在等腰梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，下列结论不一定正确的是（ ）

A．AC="BD          "   B．∠OBC=∠OCB
C．S_△AOB=S_△DOC                 D．∠BCD=∠BDC

如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
（1）求证：△MDC是等边三角形；
（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．
 

（11·天水）某校开展的一次动漫设计大赛，杨帆同学运用了数学知识
进行了富有创意的图案设计，如图（1），他在边长为1的正方形ABCD内作等边△BCE，
并与正方形的对角线交于点F、G，制作如图（2）的图标，请我计算一下图案中阴影图形的
面积．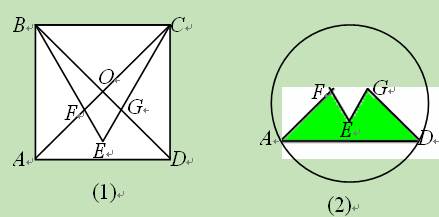

（本题6分）矩形纸片ABCD中，AB=5，AD=4．

（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是             ；（不必说明理由）
（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ，分别过点 $B$ ， $C$ 作 $\angle \mathit{BAC}$ 平分线的垂线，垂足分别为点 $D$ ， $E$ ， $\mathit{BC}$ 的中点是 $M$ ，连接 $\mathit{CD}$ ， $\mathit{MD}$ ， $\mathit{ME}$ ．则下列结论错误的是 $($ 　　 $)$

A．

$\mathit{CD}=2\mathit{ME}$

B．

$\mathit{ME}//\mathit{AB}$

C．

$\mathit{BD}=\mathit{CD}$

D．

$\mathit{ME}=\mathit{MD}$

如图，在锐角三角形 $\mathit{ABC}$中， $\mathit{AD}$是 $\mathit{BC}$边上的高，以 $\mathit{AD}$为直径的 $\odot O$交 $\mathit{AB}$于点 $E$，交 $\mathit{AC}$于点 $F$，过点 $F$作 $\mathit{FG}\perp \mathit{AB}$，垂足为 $H$，交 $\stackrel{̂}{\mathit{AE}}$于点 $G$，交 $\mathit{AD}$于点 $M$，连接 $\mathit{AG}$， $\mathit{DE}$， $\mathit{DF}$．

（1）求证： $\angle \mathit{GAD}+\angle \mathit{EDF}=180°$；

（2）若 $\angle \mathit{ACB}=45°$， $\mathit{AD}=4$， $\tan \angle \mathit{ABC}=2$，求 $\mathit{HF}$的长．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．

如图所示，已知△ABC中，AC=BC=6，∠C=90°．O是AB的中点，⊙O与AC相切于点D、与BC相切于点E．设⊙O交OB于F，连DF并延长交CB的延长线于G．

（1）∠BFG与∠BGF是否相等?为什么?
（2）求由DG、GE和所围成的图形的面积（阴影部分）．

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（   ）

A．3

B．4

C．5

D．6

已知菱形ABCD边长为5cm，tan∠DAB=,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F。若点P为AD上一点，且∠DPE+∠DAB=90⁰,则AP长为          ．

在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．
（1）如图1，△ABC和△APE均为正三角形，连接CE．
①求证：△ABP≌△ACE．
②∠ECM的度数为　   　°．
（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为　    　°．
②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为　    　°．
（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．

如图，有一块边长为4的正方形塑料摸板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是 ▲   .