如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
（1）求证：△MDC是等边三角形；
（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．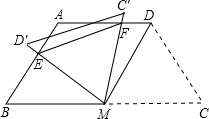
相关试题
,
,AD是△ABC的角平分线，求
的度数.
推荐套卷
如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
（1）求证：△MDC是等边三角形；
（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．
粤公网安备 44130202000953号