初中数学圆内接四边形的性质试题

如图，四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂，如此进行下去，得到四边形A_nB_nC_nD_n．
①四边形A₄B₄C₄D₄是菱形；
②四边形A₃B₃C₃D₃是矩形；
③四边形A₇B₇C₇D₇周长为；
④四边形A_nB_nC_nD_n面积为．
上述结论正确的是（     ）

A．①②③

B．②③④

C．①③④

D．①②③④

如图，把直角梯形沿方向平移得到梯形，与相交于点，=20cm，=5cm，=4cm，图中阴影部分的面积与哪个四边形的面积相等，并求出阴影部分的面积

如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC．CD上滑动，且E、F不与B．C．D重合．
（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．

某过街天桥的截面图为梯形，如图7所示，其中天桥斜面的坡度为
（是指铅直高度与水平宽度的比），的长为10m，天桥另一斜面　
坡角=.

（1）写出过街天桥斜面的坡度；
（2）求的长；
（3）若决定对该过街天桥进行改建，使斜面的坡度变缓，将其坡角改为，
方便群众，改建后斜面为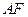.试计算此改建需占路面的宽度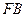的长（结果精确0.01）

我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1）），图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为、、．若正方形EFGH的边长为2，则=      ．

如图，在边长为6的正方形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N，若点M运动所经过的路程为x（6≤x≤12），那么当△ADN为等腰三角形时，x的值为___________。

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ，分别过点 $B$ ， $C$ 作 $\angle \mathit{BAC}$ 平分线的垂线，垂足分别为点 $D$ ， $E$ ， $\mathit{BC}$ 的中点是 $M$ ，连接 $\mathit{CD}$ ， $\mathit{MD}$ ， $\mathit{ME}$ ．则下列结论错误的是 $($ 　　 $)$

A．

$\mathit{CD}=2\mathit{ME}$

B．

$\mathit{ME}//\mathit{AB}$

C．

$\mathit{BD}=\mathit{CD}$

D．

$\mathit{ME}=\mathit{MD}$

如图，在锐角三角形 $\mathit{ABC}$中， $\mathit{AD}$是 $\mathit{BC}$边上的高，以 $\mathit{AD}$为直径的 $\odot O$交 $\mathit{AB}$于点 $E$，交 $\mathit{AC}$于点 $F$，过点 $F$作 $\mathit{FG}\perp \mathit{AB}$，垂足为 $H$，交 $\stackrel{̂}{\mathit{AE}}$于点 $G$，交 $\mathit{AD}$于点 $M$，连接 $\mathit{AG}$， $\mathit{DE}$， $\mathit{DF}$．

（1）求证： $\angle \mathit{GAD}+\angle \mathit{EDF}=180°$；

（2）若 $\angle \mathit{ACB}=45°$， $\mathit{AD}=4$， $\tan \angle \mathit{ABC}=2$，求 $\mathit{HF}$的长．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．

如图所示，已知△ABC中，AC=BC=6，∠C=90°．O是AB的中点，⊙O与AC相切于点D、与BC相切于点E．设⊙O交OB于F，连DF并延长交CB的延长线于G．

（1）∠BFG与∠BGF是否相等?为什么?
（2）求由DG、GE和所围成的图形的面积（阴影部分）．

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（   ）

A．3

B．4

C．5

D．6

已知菱形ABCD边长为5cm，tan∠DAB=,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F。若点P为AD上一点，且∠DPE+∠DAB=90⁰,则AP长为          ．

在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．
（1）如图1，△ABC和△APE均为正三角形，连接CE．
①求证：△ABP≌△ACE．
②∠ECM的度数为　   　°．
（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为　    　°．
②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为　    　°．
（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．

如图，有一块边长为4的正方形塑料摸板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是 ▲   .