[福建]2014年初中毕业升学考试(福建南平卷)数学
一个袋中只装有3个红球,从中随机摸出一个是红球( )
A.可能性为 |
B.属于不可能事件 | C.属于随机事件 | D.属于必然事件 |
下列计算正确的是( )
| A.(2a2)4=8a6 | B.a3+a=a4 | C.a2÷a=a | D.(a-b)2=a2-b2 |
将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是( )
| A.45° | B.60° | C.90° | D.180° |
下列说法正确的是( )
| A.了解某班同学的身高情况适合用全面调查 |
| B.数据2、3、4、2、3的众数是2 |
| C.数据4、5、5、6、0的平均数是5 |
D.甲、乙两组数据的平均数相同,方差分别是 =3.2, =3.2, =2.9,则甲组数据更稳定 =2.9,则甲组数据更稳定 |
下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
| A.1,2,1 | B.1,2,2 | C.1,2,3 | D.1,2,4 |
一名老师带领 名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为 元,则 与 的函数关系为( )
| A. | B. | C. | D. |
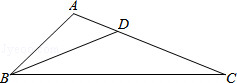
如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC=( )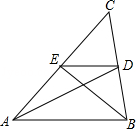
A.1:2 B.2:3 C.1:3 D.1:4
如图,将1、 、
、 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是( )
A. |
B. |
C. |
D.1 |
如图,等圆⊙O1与⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,点A在x轴的正半轴上,两圆分别与x轴交于C、D两点,y轴与⊙O2相切于点O1,点O1在y轴的负半轴上.
①四边形AO1BO2为菱形;
②点D的横坐标是点O2的横坐标的两倍;
③∠ADB=60°;
④△BCD的外接圆的圆心是线段O1O2的中点.
以上结论正确的是 .(写出所有正确结论的序号)
在2014年巴西世界杯足球赛开幕之前,某校团支部为了解本校学生对世界杯足球赛的关注情况,随机调查了部分学生对足球运动的喜欢程度,绘制成如下的两幅不完整的统计图.
请你根据以上统计图提供的信息,回答下列问题:
(1)随机抽查了 名学生;
(2)补全图中的条形图;
(3)若全校共有500名学生,请你估计全校大约有多少名学生喜欢(含“较喜欢”和“很喜欢”)足球运动.
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线.
(2)若∠A=34°,AC=6,求⊙O的周长.(结果精确到0.01)
如图,已知反比例函数y= 与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的解析式;
(2)若点D的坐标为(1,0),求△ACD的面积.
如图,已知抛物线 图象经过A(-1,0),B(4,0)两点.
图象经过A(-1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
在图1、图2、图3、图4中,点P在线段BC上移动(不与B、C重合),M在BC的延长线上.
(1)如图1,△ABC和△APE均为正三角形,连接CE.
①求证:△ABP≌△ACE.
②∠ECM的度数为 °.
(2)①如图2,若四边形ABCD和四边形APEF均为正方形,连接CE.则∠ECM的度数为 °.
②如图3,若五边形ABCDF和五边形APEGH均为正五边形,连接CE.则∠ECM的度数为 °.
(3)如图4,n边形ABC…和n边形APE…均为正n边形,连接CE,请你探索并猜想∠ECM的度数与正多边形边数n的数量关系(用含n的式子表示∠ECM的度数),并利用图4(放大后的局部图形)证明你的结论.



 .
. .
. .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号