如图,在正方形ABCD内作一个等边三角形ABE,连接DE、CE,有如下结论:①图中除等边三角形ABE外,还有三个等腰三角形;②△ADE≌△BCE;③此图形既是中心对称图形也是轴对称图形;④△ABE的面积与正方形ABCD的面积比是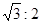 ;⑤△DEC与△ABE的面积比为
;⑤△DEC与△ABE的面积比为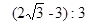 。则以上结论正确的是 .(只填正确结论的序号)
。则以上结论正确的是 .(只填正确结论的序号)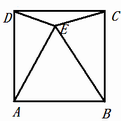
已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)如果动点E、F满足BE=CF(如图):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图),问当AE⊥BF时,点E在什么位置,并证明你的结论.
某校初四年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
观察计算:
(1)如图1,当a=4,b=1时,四边形ABFD的面积为 _________
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 _________ ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 _________ ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;
(5)综合应用:农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )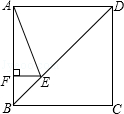
| A.1 | B.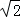 |
C.4﹣2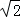 |
D.3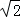 ﹣4 ﹣4 |
张大爷家有一块梯形形状的稻田(如图),已知:上底AD=400米,下底BC=600米,高h=300米,张大爷准备把这块稻田平均分给两个儿子(面积相等).
(1)分割方法有无数种,请你帮助张大爷设计两种不同的分割方案,在图1、图2中分别画出来,并简单说明理由;
(2)如果用竹篱笆将分给两个儿子的稻田隔开,问:分割线在什么位置时,所用篱笆长度最短?请在图3中画出来,并求出此时篱笆的最短长度.
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)如图②,连接DE,当t为何值时,△DEF为直角三角形?
(4)如图③,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
如图,M、N是正方形ABCD边AB、CD上两动点,连接MN,将四边形BCNM沿MN折叠,使点B落在AD边上点E处、点C落在点F.
(1)求证:BE平分∠AEF;
(2)求证:C△EDG=2AB(注:C△EDG表示△EDG的周长)
如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为 .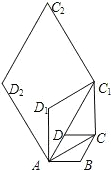
如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.
(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.
(2)引申:如果∠C≠90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C= 度时,图中阴影部分的面积和有最大值是 .
阅读理解:如图,已知直线m∥n,A、B 为直线n上两点,C、D为直线m上两点,容易证明:△ABC的面积=△ABD的面积.
根据上述内容解决以下问题:
已知正方形ABCD的边长为4,G是边CD上一点,以CG为边作正方形GCEF.
(1)如图(2), 当点G是CD的中点时,△BDF的面积为 .
(2)如图(3), 当CG = a时, 则△BDF的面积为 ,并说明理由.
探索应用:小张家有一块长方形的土地如图(4),由于修建高速公路被占去一块三角形BCP区域.现决定在DP右侧补给小张一块土地,补偿后,土地变为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形长方形ABCD的面积相等且M在射线BP上,请你在图中画出M点的位置,并简要叙述做法.
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF(S表示面积)
问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66°≈0.91,tan66°≈2.25, ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)(6,3)( ,
, )、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
如图,长方形ABCD(长方形的对边相等,每个角都是90°),AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2厘米/ 秒的速度向终点B移动,点Q以1厘米/ 秒的速度向D移动,当有一点到达终点时,另一点也停止运动。设运动的时间为t ,问:
(1)当t=1秒时,四边形BCQP面积是多少?
(2)当t为何值时,点P和点Q距离是3cm?
(3)当t= 时, 以点P、Q、D为顶点的三角形是等腰三角形.(直接写出答案)
小明遇到这样一个问题:“如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.”
分析时,小明发现,分别延长QE,MF,NG,PH交FA,GB,HC,ED的延长线于 点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个正方形(无缝隙不重叠),则这个正方形的边长为_______
(2)求正方形MNPQ的面积.
(3)参考小明思 考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ.若S△RPQ= ,则AD的长为_______.
,则AD的长为_______.