张大爷家有一块梯形形状的稻田(如图),已知:上底AD=400米,下底BC=600米,高h=300米,张大爷准备把这块稻田平均分给两个儿子(面积相等).
(1)分割方法有无数种,请你帮助张大爷设计两种不同的分割方案,在图1、图2中分别画出来,并简单说明理由;
(2)如果用竹篱笆将分给两个儿子的稻田隔开,问:分割线在什么位置时,所用篱笆长度最短?请在图3中画出来,并求出此时篱笆的最短长度.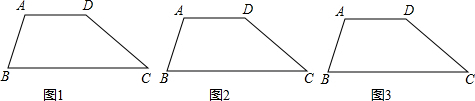
相关知识点
推荐套卷
张大爷家有一块梯形形状的稻田(如图),已知:上底AD=400米,下底BC=600米,高h=300米,张大爷准备把这块稻田平均分给两个儿子(面积相等).
(1)分割方法有无数种,请你帮助张大爷设计两种不同的分割方案,在图1、图2中分别画出来,并简单说明理由;
(2)如果用竹篱笆将分给两个儿子的稻田隔开,问:分割线在什么位置时,所用篱笆长度最短?请在图3中画出来,并求出此时篱笆的最短长度.