如图, 是 的直径, 是 的一条弦,点 是 上一点,且 , ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求直径 的长.

如图, 经过平面直角坐标系的原点 ,交 轴于点 ,交 轴于点 ,点 为第二象限内圆上一点.则 的正弦值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 的外接圆,直线 与 相切于点 , ,连接 交 于点 .
(1)求证: 平分 ;
(2)若 的平分线 交 于点 ,且 , ,求 的长.
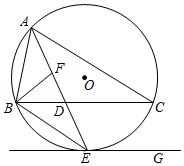
某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行研究,发现多处出现著名的黄金分割比 .如图,圆内接正五边形 ,圆心为 , 与 交于点 , 、 与 分别交于点 、 .根据圆与正五边形的对称性,只对部分图形进行研究.(其它可同理得出)
(1)求证: 是等腰三角形且底角等于 ,并直接说出 的形状;
(2)求证: ,且其比值 ;
(3)由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.

如图, 是 的直径, 是 的一条弦,点 是 上一点,且 , ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求直径 的长.

如图, 经过平面直角坐标系的原点 ,交 轴于点 ,交 轴于点 ,点 为第二象限内圆上一点.则 的正弦值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 内接于 , 是直径, ,连接 ,过点 的直线与 的延长线相交于点 ,且 .
(1)求证:直线 是 的切线;
(2)若 , ,求 的长.

如图, 为 的直径,点 ,点 是 上的两点,连接 , , .若 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
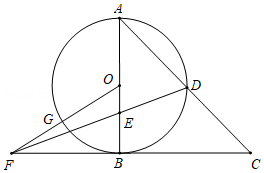
如图,在 中, , ,以 为直径的 交 于点 ,点 为线段 上的一点, ,连接 并延长交 的延长线于点 ,连接 交 于点 ,若 ,则 的长是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 的对角线 , 交于点 ,以 为直径的 经过点 ,与 交于点 , 是 延长线上一点,连接 ,交 于点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的直径.

如图, 为 的直径, , 是圆周上的两点,若 ,则锐角 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|