在平面内,给定不在同一条直线上的点,
,
,如图所示,点
到点
,
,
的距离均等于
为常数),到点
的距离等于
的所有点组成图形
,
的平分线交图形
于点
,连接
,
.
(1)求证:;
(2)过点作
,垂足为
,作
,垂足为
,延长
交图形
于点
,连接
.若
,求直线
与图形
的公共点个数.
如图, 是 的直径,点 是弦 上一动点(不与 , 重合),过点 作 ,垂足为 ,射线 交 于点 ,交过点 的切线于点 .
(1)求证: ;
(2)若 ,当 是 的中点时,判断以 , , , 为顶点的四边形是什么特殊四边形?说明理由.
如图,在四边形中,
,
,
不平行于
,过点
作
交
的外接圆
于点
,连接
.
(1)求证:四边形为平行四边形;
(2)连接,求证:
平分
.
如图,为
的直径,
为
延长线上一点,
是
的切线,
为切点,
于点
,交
于点
.
(1)求证:;
(2)若,
,求
的长.
已知:如图, 为锐角三角形, , .
求作:线段 ,使得点 在直线 上,且 .
作法:①以点 为圆心, 长为半径画圆,交直线 于 , 两点;
②连接 .
线段 就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: ,
.
,
点 在 上.
又 点 , 都在 上,
(填推理的依据).
.

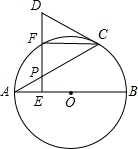
(年贵州省贵阳市)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=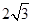 .
.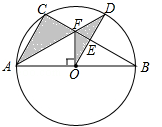
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
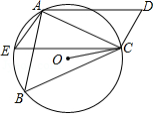
(年贵州省遵义市)如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.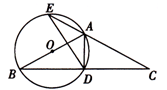
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
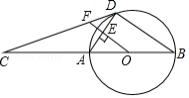
(内蒙古 呼 和 浩 特 )如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为 的中点,且∠DCF=∠P,求证:
的中点,且∠DCF=∠P,求证: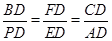

已知△ABC内接于⊙O,过点A作直线EF.
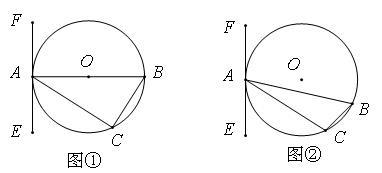
(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(要求写出两种情况): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆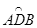 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.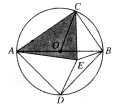
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.