初中数学圆试题

在平行四边形ABCD中，E、F分别是AB．CD的中点，连接AF、CE．
（1）求证：AF=CE；
（2）连接AC，当CA=CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．

如图，正方形ABCD中，AB＝l，BC为⊙O的直径，P是AD边上一点，BP交⊙O于点F，CF的延长线交AB于点E，连结PE．若CF＝2EF，则PF的长为          。

勾股定理有着悠久的历史，它曾引起很多人的兴趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在右图的勾股图中，已知∠ACB=90°，
∠BAC=30°，AB=4．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边_PQ上，那么△PQR的周长等于 ▲ .

如图，在直角坐标系中，点D在y轴上，四边形ABCD是等腰梯形，AB∥CD。已知， DO⊥AB， OE⊥BC，E、O分别为垂足，BC="BO" ，O为坐标原点。

(1) 求证：DO=EO
(2) 已知：C点坐标为（4 ， 8），
①求等腰梯形ABCD的腰长；
②问题探究：在这个坐标平面内是否存在点F，使以点F、D、O、E为顶点的四边形是菱形？若存在，请求出所有符合要求的F点的坐标，并说明理由；若不存在，请说明理由。

如图：在□ABCD中，对角线与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F， EF⊥AC，连结AF、CE.  

（1）求证：OE=OF
（2）请判断四边形AECF是什么特殊四边形，请证明你的结论；
（3）若∠EAF=60°，AE=6，求四边形AECF的面积.

如图，在正方形ABCD中，G是对角线AC上一点，GE⊥AB，GF⊥BC，垂足分别是E、F，连结EF、BG、DG。求证：DG=EF

如图，在梯形ABCD中，AD∥BC，AD=6厘米，BC=18厘米，E是BC的中点．点P以每秒1厘米的速度从点A出发，沿AD向点D运动；点Q同时以每秒2厘米的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当运动时间t=    ▲     秒时，以点P、E、Q、D为顶点的四边形是平行四边形．

如图，在菱形ABCD中，对角线AC与BD相交于点O，在不添加任何辅助线和字母的情况下，请添加一个条件，使其变为正方形，需要添加的条件是         ▲         ．（写出一个等式即可）

如图，矩形ABCD中，对角线AC、BD相交于点0，在BC上取BE=BO,连结AE，OE.若∠BOE
=75°，则∠CAE的度数等于（ ▲ ）．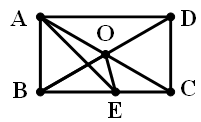

A. 30°         B.45°           C.20°         D.15°

下列命题的逆命题中，属于假命题的是（ ▲ ）．

A．两直线平行，内错角相等	B．等腰梯形的对角线相等
C．若a=b，则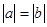	D．相等的角是对顶角

如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（ ▲ ）．

A．7

B．9

C．10

D．11

下列条件不能判定四边形ABCD是平行四边形的是（ ▲ ）．

A．AB∥CD， AD∥BC	B．AD=BC， AB=CD
C．AB∥CD， AD=BC	D．∠A=∠C ， ∠B=∠D

如图，已知菱形ABCD的边AB=10，对角线BD=12，BD边上有2012个不同的点
，过作于，于，则
的值为＿＿＿＿＿＿

下列命题，正确的是(      )

A．如果｜a｜=｜b｜，那么a=b

B．等腰梯形的对角线互相垂直

C．顺次连结四边形各边中点所得到的四边形是平行四边形

D．相等的圆周角所对的弧相等

三个正方形的位置如图所示，点在线段上，正方形的边长为4，则△的面积为  (   )

A．14

B．16

C．18

D．20