初中数学圆试题

如图，在平行四边形ABCD中，E是AD边上的中点。若∠ABE＝∠EBC ，AB＝2 ，则平行四边形ABCD的周长是         。

如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE。将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF。下列结论：①△ ABG≌△AFG；②BG＝GC；③AG∥CF；④S_△FGC＝。其中正确结论的个数是（   ）个

A．1

B．2

C．3

D．4

如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC＝3，则折痕CE的长为（   ）

A．2

B．

C．

D．6

已知梯形中位线长为5cm，面积为20cm²，则高是（   ）

A．2cm

B．4cm

C．6cm

D．8cm

下列命题中，正确的是（   ）

A．两条对角线相等的四边形是矩形

B．两条对角线互相垂直的四边形是菱形

C．两条对角线互相垂直且相等的四边形是正方形

D．两条对角线互相平分的四边形是平行四边形

如图（8），

如图（3）所示，矩形纸片中，，，现将其沿对折，使得点与点重合，则长为（   ）
 

如图，四边形中，点E在BC上，∠A＋∠ADE＝180°，∠B＝78°，∠C＝60°，求∠EDC的度数. 

已知：如图，在△ABC中，D是BC边上的一点，连结AD，取AD的中点E，过点A作BC的平行线与CE的延长线交于点F，连结DF。

（1）求证：AF=DC；
（2）若AD=CF，试判断四边形AFDC是什么样的四边形？并证明你的结论。

若菱形的两条对角线长分别为6cm，8cm，则其周长为_________cm。

如图，将一张矩形纸片对折后再对折，然后沿着图中的虚线剪下，得到①、②两部分，将②展开后得到的平面图形是(   )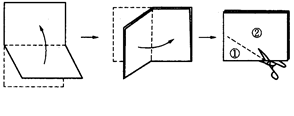

A．矩形

B．平行四边形

C．梯形

D．菱形

能判定一个四边形是菱形的条件是（    ）

A．对角线相等且互相垂直	B．对角线相等且互相平分
C．对角线互相垂直	D．对角线互相垂直平分

如图①，在Rt△ABC中，已知∠A=90°，AB=AC，G、F分别是AB、AC上的两点，且GF∥BC，AF=2，BG=4。

（1）求梯形BCFG的面积；
（2）有一梯形DEFG与梯形BCFG重合，固定△ABC，将梯形DEFG向右运动，直到点D与点C重合为止，如图②.
①若某时段运动后形成的四边形BDG'G中，DG⊥BG'，求运动路程BD的长，并求此时的值；
②设运动中BD的长度为x，试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S。

在四边形ABCD中，对角线AC、BD交于点O，从 ①AB=CD；②AB∥CD；③OA=OC；④OB=OD；⑤AC=BD；⑥∠ABC＝90°这六个条件中，可选取三个推出四边形ABCD是矩形，如①②⑤→四边形ABCD是矩形．请再写出符合要求的两个：__________________；__________________。

如图，已知AD是△ABC的中线，∠ADC＝45°，把△ABC沿AD对折，点C落在点E的位置，连接BE，若BC＝6cm。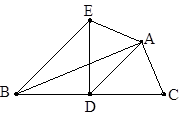

（1）求BE的长；
（2）当AD=4cm时，求四边形BDAE的面积。